个体 vs 集体
前面我们讲的 KMeans 和谱聚类都是将特征空间中的一个个个体,依据它们相互之间的关系,归属到不同的簇中。
用个形象点的比喻,我们将特征空间想象成一个二维的平面,样本数据则是“散落”在这个平面上的一颗颗“豆子”。
前面讲的聚类方法就好像:我们根据某种原则(KMeans 和谱聚类的具体原则不同),把这些“散落在地”的“豆子”捡到一个个“筐”里。
这些“豆子”原本并没有一个特定的归属,是我们在“捡”的过程中决定了把它们扔到哪个“筐”里。某一颗“豆子”被归属到某个“筐”的原因,很大程度上受它周围“豆子”归属的影响。
反过来,如果我们这么考虑问题:
在特征空间中的样本,其实都是有各自的归属的。本来一个特定的样本就应该属于一个特定的簇。
只不过,在我们拿到样本的时候,原本属于不同簇的若干样本在特征空间中“混在了一起”。
我们要做的,其实是把它们按照原本的归属区分开。
我们拿了一个西红柿,“啪”一下摔在了厨房的地板上,摔了个粉碎,于是形成了左下的一片红色“颗粒”;然后拿了一个猕猴桃,“啪”地摔成了右侧那一片绿色“颗粒”;又摔了个苦瓜,形成了左上的一片黄色颗粒。

这个时候,我们让一个小机器人来把这三种瓜果的碎屑颗粒分别收拾到三个不同的容器里。这个小机器人是个色盲,它看到的厨房地板是下图这个样子的:
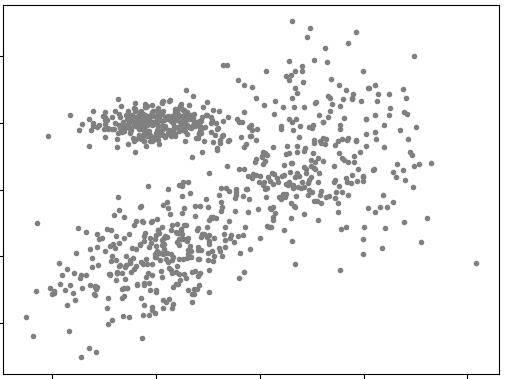
这个时候它该如何去区分三种不同瓜果的碎屑?
已知每个簇的原始分布
直观分布
当然,什么都不告诉小机器人,只让它面对一堆“灰色斑点”,那我们确实太苛刻了。
我们可以将这样一些信息泄露给小机器人:一共摔了几个瓜果,每一个的残骸形成了什么样的形状,以及其位置核心在哪里。
告诉它:地板上一共摔碎了三个瓜果,残骸分别是圆的、椭圆的和斜着的椭圆的,三片残骸的核心分别在 A,B 和 C 点(参见下图)。
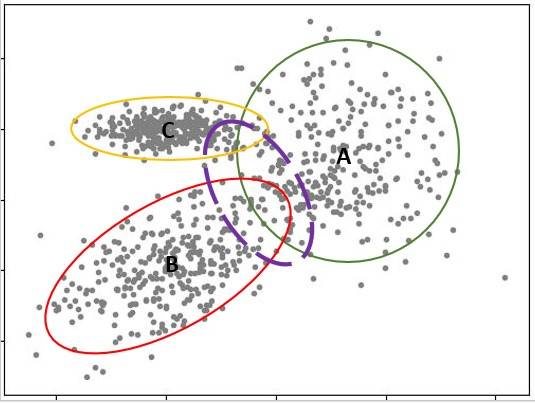
这样,小机器人在捡起一颗残骸后,就可以根据这个颗粒所在的位置,判断它在哪个瓜果的残骸区域里,从而推测它属于哪个瓜果。
形式化分布
上面描述的情景就是一个聚类问题,三堆瓜果残骸就是从直观角度可视化的分为三个簇的样本。
用形式化的方式来描述,每一个簇都有一个对应的概率分布,我们可以假定它们的概率密度函数分别是:$\phi_1(x)、\phi_2(x)$ 和 $\phi_3(x)$。
这里的 $\phi_i(·)$ 表示了一种分布形式(比如高斯分布),对于一个特定的分布而言,只有分布形式显然是不够的,还需要有参数。
这样,概率密度函数就可以写作:$\phi_i(x|\theta_i), \;\; i = 1,2, …, k$(对于上例而言,$k=3$)。
注意: $\theta_i$ 表示对应概率密度函数的参数,虽然它本身用一个字母表示,但是每一个 $\theta_i$ 实际上代表的是一个参数集合,其中包括了相应概率密度函数所需要的全部参数。
那么,当 $k$ 个分布混合起来之后,样本 $x$ 的综合概率密度为:
$P_M(x) = \sum_{i=1}^{k}\alpha_i \phi_i(x|\theta_i)$
其中 $\alpha_i > 0$, 是相对应的概率密度函数 $\phi_i(\cdot)$ 的混合系数——相当于权重,标明这个分布对最终综合分布的占比,$\sum_{i=1}^{k} \alpha_i = 1$。
对于上例而言,$\alpha_1 = \alpha_2 = \alpha_3 = \frac{1}{3}$。
已知分布条件下的样本归属
如果 $\phi_i、\theta_i$, 以及 $\alpha_i$ 都是已知的,那么对于第 $i$ 个样本 $x^{(i)}$,它归属于第 $j$ 个簇的概率为:
$P_M(c^{(i)}=j|x^{(i)}) = \frac{P(c^{(i)} = j) P_M(x^{(i)} | c^{(i)} = j)}{P_M(x^{(i)})} = \frac{\alpha_j \cdot \phi_j(x^{(i)}|\theta_j)}{\sum_{l=1}^{k} \alpha_l \cdot \phi_l(x^{(i)}|\theta_l)}$
其中 $c^{(i)}$ 表示第 $i$ 个样本的归属。
注意:这一步转换的根据是贝叶斯公式,还没忘吧?
那么,对于一个具体的样本,我们只需要计算出它归属于 $k$ 个不同簇的概率,然后选择概率值最高的那个簇作为它最终的归属即可。
比如上面的例子,对于其中大多数样本而言,对应的区域都是明确和单一的,主要是下图中紫色虚线圈中的样本,有较大的不止一种归属的可能性。

其中有些样本,可能属于 A 和 C(或者 A 和 B)的概率不是1和0的区别,而是60%和40%的区别。
这种情况下,将样本归属到概率较大的那个簇的操作,实际上是一种“软归属”(相对于 KMeans 和谱聚类的“硬归属”)。这种归属本身就带有一定的不确定性。
学习概率密度函数参数
上面说的是 $k$ 个混合在一起的分模型中,每一个概率密度函数 $\phi_i(x|\theta_i)$ 的形态及其参数都已知的情况下,使用这个已知的结果去归属一个个样本的过程。
可是,偏偏有些时候,也许参数乃至概率密度函数的形式都是未知的,这个时候该怎么办啊?
想想我们之前讲的那么多机器学习模型吧,基本都遇到过类似的情况——有一堆样本,有一个目标,有一些未知的东西,然后用一个算法把未知的部分学习出来。
我们现在也有一堆样本,也有一些未知的东西,如果也有一个目标的话,是不是可以用一个算法把未知部分学习出来?
学习目标
假设我们现在一共有 $N$ 个样本,一共有 $K$ 个簇。
我们希望:第 $i$ 个样本 $x^{(i)}$,之所以被归属到了第 $k$ 个簇,是因为 $P_M(c^{(i)}=k|x^{(i)})$ 是所有的 $P_M(c^{(i)}=l|x^{(i)}),l =1,2,…, K$ 中最大的。
我们来看看这一目标的形式化表达。
设:
$\Theta = (\theta_k)$,$Z = (z_{ik})$,$X = (x_i)$,$i=1,2, …, N$,$k = 1, 2, …, K$
其中:
$z_{ik}= \begin{cases}
\begin{array}{lr}
1, & x^{i} \ comes \ from \ the \ k^{th} \ model \\
0, & otherwise
\end{array}
\end{cases}$
我们要求取的目标为最大化样本集的集体概率:
$P(X, Z|\Theta) $
$= \prod_{i=1}^{N} P_M(x^{(i)}, z_{i1}, z_{i2}, …, z_{iK}|\Theta) $
$= \prod_{k=1}^{K}\prod_{i=1}^{N}[\alpha_k \cdot \phi_k(x^{(i)}|\theta_k)]^{z_{ik}} $
$= \prod_{k=1}^{K} \alpha_k^{n_k}\prod_{i=1}^{N} [\phi_k(x^{(i)} |\theta_k)]^{z_{ik}}$
其中:
$n_k = \sum_{i=1}^{N}z_{ik}; \;\; \sum_{k=1}^{K} n_k = N$
大家发现没有,这种连乘的形式和我们之前学习的极大似然估计的公式很像。
其实 $P(X, Z|\Theta) $ 本身就是一个似然函数。
既然是似然函数,想想之前我们在学习朴素贝叶斯模型时,是怎么来优化似然函数的?我们采取的是极大化对数似然函数的方法。
同样的方法,是否可以用到此处呢?
我们先来看看这里的对数似然函数,它是这个样子的:
对于给定样本集 $D$,它的混合模型聚类的对数似然函数为:
$LL(D) = LL(\Theta|X,Z) = \log{P(X, Z|\Theta) } = \sum_{k=1}^{K}[n_k \log{\alpha_k} + \sum_{i=1}^{N} z_{ik} \log{(\phi_k(x^{(i)}|\theta_k))}] $
我们的学习目标就是极大化 $LL(\Theta|X,Z) $。
同分布的混合模型
我们的学习目标是:
$ \arg\max{LL(\Theta|X,Z) } = \arg{\max{ [ \sum_{k=1}^{K}[n_k \log{\alpha_k} + \sum_{i=1}^{N} z_{ik} \log{(\phi_k(x^{(i)}|\theta_k))}] }}$
看起来好像不是很难啊,可是不要忘记了,这里面的每个 $\phi_k(x|\theta_k)$ 都是一个独立的概率密度函数形式,而 $\theta_k$ 是对应的参数集合!
如果 $K$ 个分模型的概率分布都不相同——每个概率密度函数的形式不同,对应参数集合不同,参数本身又都是未知的——那可怎么求解呀?!简直就是一场灾难啊!
好在我们没有那么倒霉,不用非得去求这样挑战极限的模型混合模式。
我们只需要把所有的 $\phi_k(x|\theta_k)$ 都当作高斯分布即可。也就是说这些样本分属的模型对应的概率密度函数形式相同,参数类型也相同,只是参数的具体取值有所差别。
所谓高斯混合模型(GMM),顾名思义,就是将若干个概率分布为高斯分布的分模型混合在一起的模型。
在具体讲解 GMM 之前,先回顾一下高斯分布。
高斯混合模型(GMM)
高斯分布的混合
鉴于高斯分布的广泛应用和独特性质,将它作为概率分布分模型混合出来的模型,自然可以处理很多的实际问题。
比如上边的例子:
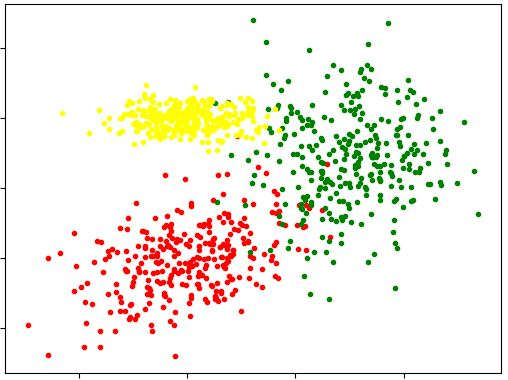
这里面的三个混合在一起的簇,无论原本每一簇自身的分布如何,我们都可以用高斯模型来近似表示它们。
因此整个混合模型,也就可以是一个高斯混合模型(GMM)——用高斯密度函数代替上一篇给出的混合模型中的 $\phi_k(\cdot)$,也就是:
$\phi_k(x|\mu_k, {\sigma^2}_k) = \frac{1}{\sqrt{2\pi{\sigma^2}_k}} \ \exp \left( -\frac{(x- \mu_k)^2}{2{\sigma^2}_k} \right)$,
$\theta_k = (\mu_k, {\sigma^2}_k)$。
则 GMM 的形式化表达为:
$P(x|\theta) = \sum_{k=1}^{K}\alpha_k \cdot \phi_k(x | \theta_k) = \sum_{k=1}^{K} \frac{\alpha_k}{\sqrt{2\pi{\sigma^2}_k}} \ \exp \left( -\frac{(x- \mu_k)^2}{2{\sigma^2}_k} \right)$
其中,$\alpha_k$ 是系数,$ \alpha_k \geqslant 0$,$\sum_{k=1}^{K}\alpha_k = 1$。
GMM 的对数似然函数
混合模型的学习目标为:
$\arg\min{LL(\Theta|X,Z)}$
套用上一节已经给出的对数似然函数的形式,GMM 的对数似然函数为:
$LL(\Theta|X,Z) = \log{P(X,Z|\Theta)} $
$= \sum_{k=1}^{K}[n_k \log{\alpha_k} + \sum_{i=1}^{N} z_{ik} \log{(\phi_k(x^{(i)}|\theta_k))}] $
$= \sum_{k=1}^{K}[n_k \log{\alpha_k} + \sum_{i=1}^{N} z_{ik} [\log{(\frac{1}{\sqrt{2\pi}})} - \frac{1}{2}\log{{\sigma^2}_k} - \frac{1}{2{\sigma^2}_k}(x^{(i)} - \mu_k)^2]]$
其中:$\Theta = (\theta_k)$,$X = (x_i)$,$Z = (z_{ik})$。
$z_{ik}= \begin{cases}
\begin{array}{lr}
1, & \mbox{第i个样本x^{(i)}来自第k个分模型} \\
0, & \mbox{否则}
\end{array}
\end{cases}$
$i=1,2, …, N$;$ k = 1, 2, …, K$;
并有 $n_k = \sum_{i=1}^{N}z_{ik}$;$ \sum_{k=1}^{K} n_k = N$。
现在的这个对数似然函数中,$x^{(i)}$ 是已经观测到的样本观测数据,是已知的,$z_{ik}$ 却是未知的。
训练样本是“不完整的”,有没被观测到的隐变量(Hidden Variable)存在,这样的对数似然函数需要用之前学过的 EM 算法来优化。
用 EM 算法学习 GMM 的参数
将 EM 算法应用于 GMM
最优化 GMM 目标函数的过程就是一个典型的 EM 算法,一共分为4步:
- 各参数取初始值开始迭代;
- E 步;
- M 步;
- 重复 E 步和 M 步,直到收敛。
过程清晰明确,关键就是 E 步和 M 步的细节。
GMM 的 E 步
E 步的任务是求 $Q(\Theta,\Theta^t)$。
按照 EM 算法的描述:
$Q(\Theta,\Theta^t) = E_{Z | X, \Theta^t}LL(\Theta|X,Z) = E_{Z | X, \Theta^t}[\log{P(X,Z|\Theta)}] $
其中 $Z$ 为隐变量。
在 GMM 中,隐变量为 $Z = (z_{ik}), \ \ i=1,2, …, N; k = 1, 2, …, K$。
因此:
$Q(\Theta,\Theta^t) $
$= E_{Z | X, \Theta^t}[\log{P(X, Z|\Theta)}] $
$ = E_{Z | X, \Theta^t}\{ \sum_{k=1}^{K}[n_k \log{\alpha_k} + \sum_{i=1}^{N} z_{ik} \log{(\phi_k(x^{(i)}|\theta_k))}]\}$
$=E_{Z | X, \Theta^t}\{ \sum_{k=1}^{K}[n_k \log{\alpha_k} + \sum_{i=1}^{N} z_{ik} [\log{(\frac{1}{\sqrt{2\pi}})} - \log{\sigma_k} - \frac{1}{2\sigma_k^2}(x^{(i)} - \mu_k)^2]]\} $
$ = \sum_{k=1}^{K}[\sum_{i=1}^n E(z_{ik}|X, \Theta^t) \log{\alpha_k} + \sum_{i=1}^{N} E(z_{ik}|X, \Theta^t) [\log{(\frac{1}{\sqrt{2\pi}})} - \log{\sigma_k} - \frac{1}{2\sigma_k^2}(x^{(i)} - \mu_k)^2]]$
$E(z_{ik}|X, \Theta^t)$ 是当前模型参数 $\Theta^t$ 下,第 $i$ 个观测数据——$x^{(i)}$——来自第 $k$ 个分类的概率期望。
$E(z_{ik}|X, \Theta^t)$ 又叫做分模型 $k$ 对观测数据 $x^{(i)}$ 的影响度。这里需要计算它,为了方便表示,记作 $\hat{z_{ik}}$。
$\hat{z_{ik}} = P(z_{ik} = 1| X, \Theta^t) $
$= \frac{P(z_{ik} = 1, x^{(i)} | \Theta^t)}{\sum_{k=1}^{K} P(z_{ik} = 1, x^{(i)} | \Theta^t)} $
$= \frac{P( x^{(i)} |z_{ik} = 1, \Theta^t)P(z_{ik} = 1|\Theta^t)}{\sum_{k=1}^{K} P(x^{(i)} | z_{ik} = 1, \Theta^t)P(z_{ik} = 1|\Theta^t)} $
$= \frac{\alpha_k^t \phi(x^{(i)}|\theta_k^t)}{\sum_{k=1}^{K} \alpha_k^t \phi(x^{(i)}|\theta_k^t)} $
其中,$i = 1,2,..., N$;$k = 1,2,..., K$。
这里的 $x^{(i)}$ 是样本观测值,$\alpha_k^t$ 和 $\theta_k^t$ 是上一个迭代的 M 步计算出来的参数估计值,都是已知的,因此可以直接求解 $\hat{z_{ik}} $ 的值。
求出 $\hat{z_{ik}}$ 的解后,再将 $\hat{z_{ik}} = E(z_{ik}|X, \Theta^t)$ 以及 $n_k = \sum_{i=1}^{N} E(z_{ik}|X, \Theta^t)$ 代回到 $Q(\Theta,\Theta^t) $式子里,得到:
$Q(\Theta,\Theta^t) = \sum_{k=1}^{K}\{n_k\log{\alpha_k} + \sum_{i=1}^{N}\hat{z_{ik}} [\log{(\frac{1}{\sqrt{2\pi}})} - \log{\sigma_k} - \frac{1}{2\sigma_k^2}(x^{(i)} - \mu_k)^2]\}$
至此 $Q(\Theta,\Theta^t)$ 成了关于 $ \alpha_k$ 和 $\theta_k =( \mu_k, {\sigma^2}_k)$ 的函数,其中 $k = 1,2, ..., K$。
GMM 的 M 步
M 步的任务是: $\arg{\max_{\Theta} {Q(\Theta,\Theta^t)}}$。
根据上一步得出的结果,我们看到 $Q(\Theta,\Theta^t) $ 里面含有未知的参数 $\alpha_k, \mu_k, {\sigma^2}_k, k = 1,2, ..., K$。
我们可以把这一步的任务看作是极大化一个包含着若干自变量的函数,那么就拿出我们惯常的办法——通过分别对各个自变量求偏导,再令导数为0,来求取各自变量的极值,然后再带回到函数中去求整体的极值。
注意:采用这种办法要注意,对 $\mu_k$ 和 $\sigma_k^2$ 直接求偏导,并令其为$0$即可。
对于 $\alpha_k$ 是在 $\sum_{k=1}^{K} \alpha_k = 1$ 的条件下求偏导数,此处可用拉格朗日乘子法。
最后得出表示 $\Theta_{t+1}$ 的各参数的结果为:
${\mu_k}^{t+1} = \frac{\sum_{i=1}^{N} \hat{z_{ik}} x^{(i)}}{ \sum_{i=1}^{N} \hat{z_{ik}}}, \ \ k=1,2,..., K$
${{\sigma^2}_k}^{t+1} = \frac{\sum_{i=1}^{N} \hat{z_{ik}} (x^{(i)} - \mu_k^{t+1})^2}{ \sum_{i=1}^{N} \hat{z_{ik}}}, \ \ k=1,2,..., K$
${\alpha_k}^{t+1} = \frac{n_k}{N} = \frac{\sum_{i=1}^{N} \hat{z_{ik}}}{N}, \ \ k=1,2,..., K$
GMM 实例
下面我们来看一个 GMM 的例子:
from matplotlib.pylab import array,diag
import matplotlib.pyplot as plt
import matplotlib as mpl
import pypr.clustering.gmm as gmm
import numpy as np
from scipy import linalg
from sklearn import mixture
# 将样本点显示在二维坐标中
def plot_results(X, Y_, means, covariances, colors, eclipsed, index, title):
splot = plt.subplot(2, 1, 1 + index)
for i, (mean, covar, color) in enumerate(zip(
means, covariances, colors)):
v, w = linalg.eigh(covar)
v = 2. * np.sqrt(2.) * np.sqrt(v)
u = w[0] / linalg.norm(w[0])
# as the DP will not use every component it has access to
# unless it needs it, we shouldn't plot the redundant
# components.
if not np.any(Y_ == i):
continue
plt.scatter(X[Y_ == i, 0], X[Y_ == i, 1], .8, color=color)
if eclipsed:
# Plot an ellipse to show the Gaussian component
angle = np.arctan(u[1] / u[0])
angle = 180. * angle / np.pi # convert to degrees
ell = mpl.patches.Ellipse(mean, v[0], v[1], 180. + angle, color=color)
ell.set_clip_box(splot.bbox)
ell.set_alpha(0.5)
splot.add_artist(ell)
plt.xticks(())
plt.yticks(())
plt.title(title)
#创建样本数据,一共3个簇
mc = [0.4, 0.4, 0.2]
centroids = [ array([0,0]), array([3,3]), array([0,4]) ]
ccov = [ array([[1,0.4],[0.4,1]]), diag((1,2)), diag((0.4,0.1)) ]
X = gmm.sample_gaussian_mixture(centroids, ccov, mc, samples=1000)
#用plot_results函数显示未经聚类的样本数据
gmm = mixture.GaussianMixture(n_components=1, covariance_type='full').fit(X)
plot_results(X, gmm.predict(X), gmm.means_, gmm.covariances_, ['grey'],False, 0, "Sample data")
#用EM算法的GMM将样本分为3个簇,并按不同颜色显示在二维坐标系中
gmm = mixture.GaussianMixture(n_components=3, covariance_type='full').fit(X)
plot_results(X, gmm.predict(X), gmm.means_, gmm.covariances_, ['red', 'blue', 'green'], True, 1, "GMM clustered data")
plt.show()
最后的显示结果如下:
注意:上面代码中用到了 PyPR 聚类包,该包基于 Python 2 实现。使用命令:pip3 install pypr,可以对其进行安装,但如果在Python 3 环境中调用该命令,需手动修改 gmm.py 文件中的代码,使其符合 Python 3 语法才可以。你可以尝试自己修改 gmm.py。
如果你使用的是 pypr-0.1.1,可以用以下网址中下载的 gmm.py 文件替换该目录(...\Python36\Lib\site-packages\pypr\clustering\gmm.py)下的 gmm.py。
https://github.com/gadzan/MachineLearningResource/blob/master/gmm/gmm.py
如果报错ModuleNotFoundError: No module named 'xxxx'在相应行的import前加上from .变成from . import xxxx。
其他实现Github em-gaussian


