贝叶斯方差方法
允许的假设越复杂,数据错误率越低,越能拟合数据;
但是在现实中,有关未知数据的泛化误差,形成一个反抛物线,它是训练数据误差与另一个名为过拟合误差的函数之和;
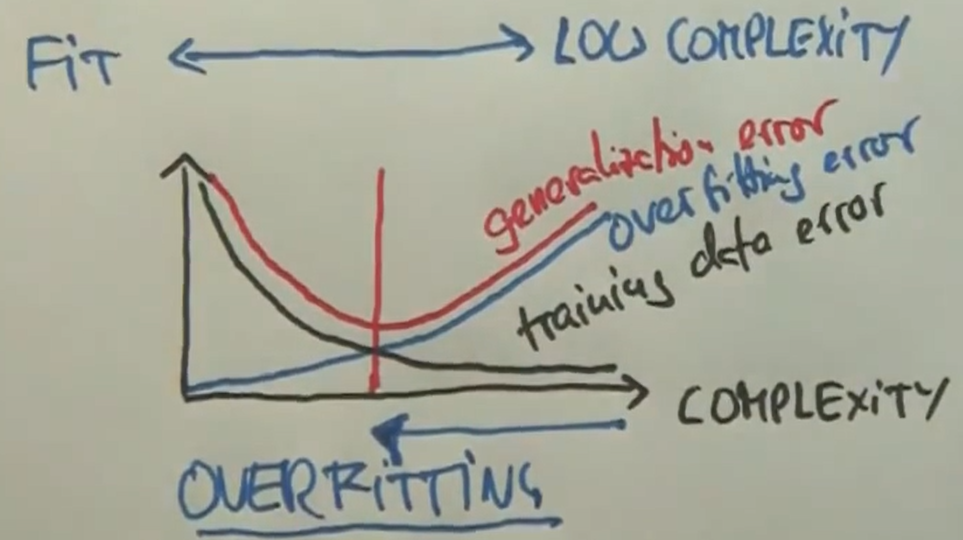
在泛化误差最小的情况下,可获得最佳复杂性
选择复杂性低一些的模型,你的算法往往表现的更好
贝叶斯网络 进行 垃圾邮件检测
词袋
我们一起学猫叫
一起喵喵喵喵喵
| 我们 | 一起 | 学 | 猫叫 | 喵 |
|---|---|---|---|---|
| 1 | 2 | 1 | 1 | 5 |
垃圾信息
优惠满减活动
打折优惠活动
有效信息
短信验证码
邮件验证码
词汇量
|优惠|满减|活动|打折|短信|邮件|验证码|
共7个
分类回归问题
分类算法的特点是目标标签或目标是离散的
{0,1}
回归算法可以预测连续的变化,例如明天温度,
[0, 1]
线性回归
Y = WX + V
|X|Y|
|3|0|
|6|-3|
|4|-1|
|5|-2|
不进行数学计算推理出,
当X:3->6时 Y:0->-3, 变化X+3, Y-3
当X:3->4时 Y:0->-1, 变化X+1, Y-1
当X:3->5时 Y:0->-2, 变化X+2, Y-2
那么W=-1, V=3
损失函数
尽可能正确地拟合线性函数后
可通过损失函数求出残差量
计算残差要对所有训练样本求和
Y = F(x)
LOSS = ∑γ(Yγ - WXγ - V)²

