贝叶斯定理
公式:$P(A|B) =\frac{ P(B|A) P(A)}{P(B)}$
在 B 出现的前提下 A 出现的概率,等于 A 和 B 都出现的概率除以 B 出现的概率
一般化的贝叶斯公式:
假设事件 A 本身又包含多种可能性,即 A 是一个集合 $A = {A_1, A_2, …, A_n}$,那么对于集合中任意的 $A_i$
$P(A_i|B) = \frac{P(B|A_i) P(A_i)}{\sum_{j}P(B|A_j)P(A_j)}$
朴素贝叶斯分类器(Naïve Bayes Classifier)
$P(A|B)$ 可以写为:
$P(A|b_1,b_2,…, b_n) =\frac{ P(A) P(b_1, b_2, …, b_n | A) }{ P(b_1, b_2, …, b_n)}$
每个特征 $b_i$ 与其他特征都不相关,则有
$P(A|b_1,b_2,…, b_n) =\frac{1}{Z}P(A) \prod_{i=1}^{n} P(b_i|A)$
Z 为$P(b_1, b_2, …, b_n)$
换种写法就是
朴素贝叶斯分类器的模型函数
$P(C|F_1,F_2,…, F_n) =\frac{1}{Z}P(C) \prod_{i=1}^{n} P(F_i|C)$
假设我们当前有一个模型,
总共只有两个类别:$c_1$ 和 $c_2$;
有三个 Feature:$F_1、F_2 和 F_3$。
$F_1$ 有两种可能性取值:$f_{11}$ 和 $f_{12}$;
$F_2$ 有三种可能性取值:$f_{21}、f_{22}、f_{23}$;
$F_3$ 也有两种可能性取值:$f_{31}、f_{32}$
那么对于这个模型,我们要做的就是通过训练过程,获得下面这些值:
$P(C = c_1)$
$P(C = c_2)$
$P(F_1=f_{11} | C=c_1)$
$P(F_1=f_{12} | C=c_1)$
$P(F_2=f_{21} | C=c_1)$
$P(F_2=f_{22} | C=c_1)$
$P(F_2=f_{23} | C=c_1)$
$P(F_3=f_{31} | C=c_1)$
$P(F_3=f_{32} | C=c_1)$
$P(F_1=f_{11} | C=c_2)$
$P(F_1=f_{12} | C=c_2)$
$P(F_2=f_{21} | C=c_2)$
$P(F_2=f_{22} | C=c_2)$
$P(F_2=f_{23} | C=c_2)$
$P(F_3=f_{31} | C=c_2)$
$P(F_3=f_{32} | C=c_2)$
比如我们有一个需要预测的样本 X,它的特征值分别是 $f_{11}、f_{22}、f_{31}$,那么:
样本 $X$ 被分为 $c_1$ 的概率是:$P(C=c_1|x) = P(C=c_1| F_1=f_{11}, F_2=f_{22}, F_3=f_{31}) \propto P(C=c_1)P(F_1=f_{11} | C=c_1)P(F_2=f_{22} | C=c_1)P(F_3=f_{31} | C=c_1) ;$
样本 $X$ 被分为 $c_2$ 的概率是:$P(C=c_2|x) = P(C=c_2| F_1=f_{11}, F_2=f_{22}, F_3=f_{31}) \propto P(C=c_2)P(F_1=f_{11} | C=c_2)P(F_2=f_{22} | C=c_2)P(F_3=f_{31} | C=c_2)$
对比 $P(C=c_1|x) 和 P(C=c_2|x)$ 谁更大,那么这个样本的预测值就是对应类别。
假设 $P(C=c_2|x)$ > $P(C=c_1|x)$,则 x 的预测值为 $c_2$,这个样本被分类器分为了 $c_2$。
高斯分布
高斯分布密度函数
高斯分布(Gaussian Distribution),又名正态分布(Normal distribtion),它的密度函数为:
$f(x;\mu,{\sigma^2}) = \frac{1}{\sqrt{2\pi{\sigma^2}}} \ \exp \left( -\frac{(x- \mu)^2}{2\sigma^2} \right)$
分布形式如下图(四个不同参数集的高斯分布概率密度函数):
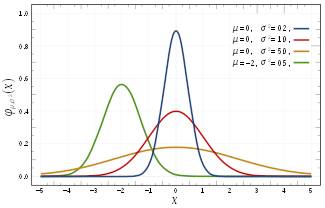
高斯分布的概率密度函数曲线呈钟形,因此人们经常将其称之为钟形曲线(类似于寺庙里的大钟,因此得名)。
图中红色曲线是 $\mu =0$、$\sigma^2 = 1$ 的高斯分布,这个分布有个专门的名字:标准高斯分布。
常见的分布
高斯分布是一种非常常见的概率分布,经常被用来定量自然界的现象。
现实生活中的许多自然现象都被发现近似地符合高斯分布,比如人类的寿命、身高、体重、智商等和我们生活息息相关的数据。
不止是人类体征或者生物特征,在金融、科研、工业等各个领域都有大量现实业务产生的数据被证明是符合高斯分布的。
中心极限定理
高斯分布的重要性质
高斯分布有一个非常重要的性质:在适当的条件下,大量相互独立的随机变量的均值经适当标准化后,依分布收敛于高斯分布(即使这些变量自己的分布并不是高斯分布)——这就是中心极限定理。
严格说起来,中心极限定理并不是一个定理,而是一类定理。
这类定理从数学上证明了:在自然界与人类生产活动中,一些现象受到许多相互独立的随机因素的影响,当每个因素所产生的影响都很微小时,总的影响可以看作是服从高斯分布的。
经典中心极限定理
中心极限定理中,最常用也最简单的是经典中心极限定理,这一定理说明了什么,我们看下面的解释。
设 $(x_1, …, x_n)$ 为一个独立同分布的随机变量样本序列,且这些样本值的期望为 $\mu$,有限方差为 $\sigma^2 $。
$S_n$ 为这些样本的算术平均值:
$S_{n} ={\frac {x_{1}+\cdots +x_{n}}{n}}$
注意:一般情况下 $n \geqslant 30$,而 $\mu$ 是 $S_n$ 的极限。
随着 $n$ 的增大,$\sqrt{n}(S_n − \mu)$ 的分布逐渐近似于均值为 $0$、方差是 $\sigma^2$ 的高斯分布,即:
${\sqrt {n}}\left(S_{n}-\mu \right)\ {\xrightarrow {d}}\ N\left(0,\sigma ^{2}\right)$
也就是说,无论 $x_i$ 的自身分布是什么,随着 $n$ 变大,这些样本平均值经过标准化处理——$\sqrt{n}(S_n − \mu)$——后的分布,都会逐步接近高斯分布。
一个例子
定理说起来有点抽象,我们来看一个例子就明白了。
我们用一个依据均匀概率分布生成数字的生成器,来生成$0$到$100$之间的数字。
生成器每次运行都连续生成 $N$ 个数字——我们将每次运行称为一次“尝试”。
我们让这个生成器连续尝试$500$次,每次尝试后都计算出本次生成的 N 个数字的均值。
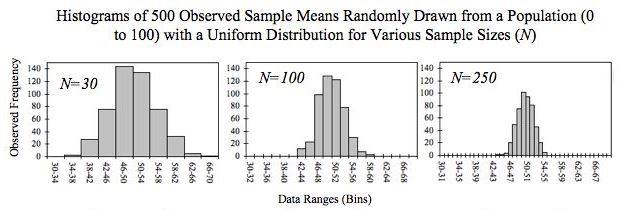
最后,将$500$次的统计结果放入二维坐标系,$x$ 轴(横轴)表示一次尝试中 $N$ 个数字的均值,而 $y$ 轴(纵轴)表示均值为 $x$ 的尝试出现的次数(观察频次,Observed Frenquncy)。
下图展示了 $N=30、N=100$ 和 $N=250$ 时的三种情况。直观可见,分布基本上都是钟形曲线,而且 $N$ 越大,曲线越平滑稳定。
另一个例子
再来看一个抛硬币的例子,这是最早发现的中心极限定理的特例,由法国数学家棣莫弗(Abraham de Moivre)发表在1733年出版的论文里。
一个人掷硬币,每次 TA 都一下子抛出一大把 $n$ 枚硬币,然后统计落地后“头”(Head,印有人头像的一面)朝上硬币出现的个数。
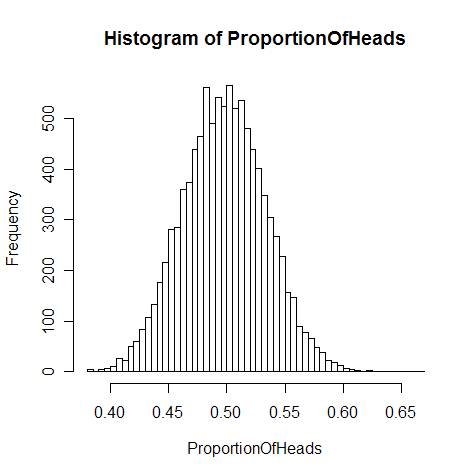
总共抛掷很多次,那么这一系列投掷活动中硬币“头”朝上的可能性($ProportionOfHeads = \frac{每次正面朝上个数}{n}$)将形成一条高斯曲线(如下图):
近似为高斯分布
中心极限定理是数理统计学和误差分析的理论基础,指出了大量随机变量之和近似服从高斯分布的条件。
这一定理的重要性在于:根据它的结论,其他概率分布可以用高斯分布作为近似。
例如:
-
参数为 $n$ 和 $p$ 的二项分布,在 $n$ 相当大而且 $p$ 接近 $0.5$ 时,近似于 $\mu = np$、$\sigma^2 = np (1 - p)$ 的高斯分布。
-
参数为 $\lambda$ 的泊松分布,当取样样本数很大时,近似于 $\mu = \lambda$、$\sigma^2 = \lambda$ 的高斯分布。
这就使得高斯分布在事实上成为了一个方便模型——如果对某一变量做定量分析时其确定的分布情况未知,那么不妨先假设它服从高斯分布。
如此一来,当我们遇到一个问题的时候,只要掌握了大量的观测样本,都可以按照服从高斯分布来处理这些样本。
极大似然估计 (Maximum Likelihood Estimation, MLE)
假设$P(x_i |c)$ 符合高斯分布,则:
$P(x_i|c) = \frac{1}{{ \sqrt {2\pi \sigma_{c,i}^2 } }}exp( \frac{-(x_i - \mu_{c,i})^2 }{{2\sigma_{c,i} ^2 }}) $
高斯分布由两个参数——均值和方差,即上式中的 $\mu_{c,i}$ 和 $\sigma_{c,i}$ 决定,也就是说 $\theta_{c,i} = (\mu_{c,i} ,\sigma_{c,i} )$
$D_c$ 是训练集中所有被分类为 $c$ 的样本的集合,其中样本数量为 $m_c$;每一个样本都有 $n$ 个特征;每一个特征有一个对应的取值。我们将第 $j$ 个样本的第 $i$ 个特征值记作:$x_i^{(j)}$。
假设 $P(x_i | c)$ 符合某一种形式的分布,该分布被参数 $\theta_{c,i}$ 唯一确定。为了明确起见,我们把 $P(x_i | c)$ 写作 $P(x_i | \theta_{c,i})$。
现在,我们要做的是,利用 $D_c$ 来估计参数 $\theta_{c,i}$。
参数 $\theta_{c,i}$ 的似然函数记作 $L(\theta_{c,i})$,它表示了 $D_c$ 中的 $m_c$ 个样本 $X_1,X_2,… X_{m_c}$ 在第 $i$ 个特征上的联合概率分布1:
$L(\theta_{c,i}) = \prod_{j=1}^{m_c} P(x_i^{(j)}|\theta_{c,i})$
1.[联合概率分布]举例说明:打靶时命中的坐标(x,y)的概率分布就是联合概率分布(涉及两个随机变量)
极大似然估计,就是去寻找让似然函数 $L(\theta_{c,i})$ 的取值达到最大的参数值的估计方法。
让 $L(\theta_{c,i} ) $ 达到最大的参数值记作 $\theta_{c,i}^* $。则 $\theta_{c,i}^* $ 满足这样的情况:
- 将 $\theta_{c,i}^* $ 带入到 $P(x_i|c)$ 的分布形式中去,确定了唯一的一个分布函数 $ f(x)$ (比如这个 $f(x)$ 是一个高斯函数,$\theta_{c,i}^* $ 对应的是它的均值和方差);
- 将 $D_c$ 中每一个样本的第 $i$ 个特征的值带入到 $f(x)$ 中,得到的结果是一个 [0,1] 之间的概率值,将所有 $m_c$ 个 $f(x)$ 的计算结果累计相乘,最后得出的结果是最大的。
求取 $\theta_{c,i}^* $ 的过程,就是最大化 $L(\theta_{c,i})$ 的过程:
$\theta_{c,i}^* = argmax L(\theta_{c,i})$
对上面等式取对数,得到 $\theta_{c,i}$ 的对数似然:
$LL(\theta_{c,i}) = \sum_{j=1}^{m_c} log(P(x_i^{(j)}|\theta_{c,i})) $
最大化一个似然函数同最大化它的自然对数是等价的
正态分布的极大似然估计
$LL(\theta_{c,i}) = LL(\mu_{c,i}, \sigma_{c,i}^2) = \sum_{j=1}^{m_c} log(\frac{1}{{ \sqrt {2\pi \sigma_{c,i}^2 } }}exp( \frac{-(x_i^{(j)} - \mu_{c,i})^2 }{{2\sigma_{c,i} ^2 }})) $
$\theta_{c,i} = (\mu_{c,i}, \sigma_{c,i} ^ 2)$
对 $\mu_{c,i}$ 求偏导:$\frac{\partial{ LL(\mu_{c,i}, \sigma_{c,i}^2)}}{\partial{\mu_{c,i}}} = \sum_{j=1}^{m_c}( \frac{x_i^{(j)} - \mu_{c,i} }{{\sigma_{c,i} ^2 }}) $
令: $\frac{\partial{ LL(\mu_{c,i}, \sigma_{c,i}^2)}}{\partial{\mu_{c,i}}} = 0 $
则: $\sum_{j=1}^{m_c}( \frac{x_i^{(j)} - \mu_{c,i} }{{\sigma_{c,i} ^2 }}) = 0 $
有: $\mu_{c,i} = \frac{1}{m_c} \sum_{j=1}^{m_c}(x_i^{(j)}) $
然后对 $\sigma_{c,i}$ 求偏导:
$\frac{\partial{ LL(\mu_{c,i}, \sigma_{c,i}^2)}}{\partial{\sigma_{c,i}^2}} = \sum_{j=1}^{m_c}(\frac{-1}{2\sigma_{c,i}^2} + \frac{(x_i^{(j)} - \mu_{c,i})^2}{2\sigma_{c,i}^2\sigma_{c,i}^2}) $
令: $\sum_{j=1}^{m_c}(\frac{-1}{2\sigma_{c,i}^2} + \frac{(x_i^{(j)} -\mu_{c,i})^2}{2\sigma_{c,i}^2\sigma_{c,i}^2}) = 0 $
最后得出:
$\sigma_{c,i}^2 = \frac{1}{m_c} \sum_{j=1}^{m_c}(x_i^{(j)} - \mu_{c,i})^2 $
用代码实现朴素贝叶斯模型
import pandas as pd
import numpy as np
import time
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
# Importing dataset.
# Please refer to the 【Data】 part after the code for the data file.
data = pd.read_csv("career_data.csv")
# Convert categorical variable to numeric
data["985_cleaned"]=np.where(data["985"]=="Yes",1,0)
data["education_cleaned"]=np.where(data["education"]=="bachlor",1,
np.where(data["education"]=="master",2,
np.where(data["education"]=="phd",3,4)
)
)
data["skill_cleaned"]=np.where(data["skill"]=="c++",1,
np.where(data["skill"]=="java",2,3
)
)
data["enrolled_cleaned"]=np.where(data["enrolled"]=="Yes",1,0)
# Split dataset in training and test datasets
X_train, X_test = train_test_split(data, test_size=0.1, random_state=int(time.time()))
# Instantiate the classifier
gnb = GaussianNB()
used_features =[
"985_cleaned",
"education_cleaned",
"skill_cleaned"
]
# Train classifier
gnb.fit(
X_train[used_features].values,
X_train["enrolled_cleaned"]
)
y_pred = gnb.predict(X_test[used_features])
# Print results
print("Number of mislabeled points out of a total {} points : {}, performance {:05.2f}%"
.format(
X_test.shape[0],
(X_test["enrolled_cleaned"] != y_pred).sum(),
100*(1-(X_test["enrolled_cleaned"] != y_pred).sum()/X_test.shape[0])
))
career_data.csv
no,985,education,skill,enrolled
1,Yes,bachlor,C++,No
2,Yes,bachlor,Java,Yes
3,No,master,Java,Yes
4,No,master,C++,No
5,Yes,bachlor,Java,Yes
6,No,master,C++,No
7,Yes,master,Java,Yes
8,Yes,phd,C++,Yes
9,No,phd,Java,Yes
10,No,bachlor,Java,No

