回顾一下微分
- 函数中某一点的斜率
- 函数的变化率
下面是几个常见的微分方程
一元函数微分方程
$\frac{\mathrm{d}(x^2) }{\mathrm{d} x} = 2x \\
\frac{\mathrm{d}(-2y^5) }{\mathrm{d} y} = -10y^4 \\
\frac{\mathrm{d}(5-\theta)^2 }{\mathrm{d} \theta} = -2(5-\theta)(negative \ sign \ coming \ from \ -\theta)$
多元函数微分方程,对每个变量进行微分
$\frac{\partial}{\partial x}(x^2y^2)=2xy^2 \\
\frac{\partial}{\partial y}(-2y^5+z^2)=-10y^4 \\
\frac{\partial}{\partial \theta_2}(5\theta_1+2\theta_2-12\theta_3)= 2 \
\frac{\partial}{\partial \theta_2}(0.55-(5\theta_1+2\theta_2-12\theta_3)) = -2$
什么是梯度
梯度实际上是多元函数的微分,下面用$J(\theta_1,\theta_2,\theta_3)$举例:
$J(\Theta) = 0.55-(5\theta_1+2\theta_2-12\theta_3) \\
\triangledown J(\Theta)=\left \langle \frac{\partial J}{\partial \theta_1}, \frac{\partial J}{\partial \theta_2}, \frac{\partial J}{\partial \theta_3} \right \rangle \\
= \left \langle -5,-2,-12 \right \rangle$
$\triangledown$是梯度的符号,$\left \langle \right \rangle$包裹起来的部分代表这是一个向量
下面是稍微复杂一点的例子:
$J(\Theta) = \frac{1}{2}(0.55-(5\theta_1+2\theta_2-12\theta_3))^2 \
\triangledown J(\Theta)=\left \langle \frac{\partial J}{\partial \theta_1}, \frac{\partial J}{\partial \theta_2}, \frac{\partial J}{\partial \theta_3} \right \rangle \
= \left \langle -5(0.55-(5\theta_1+2\theta_2-12\theta_3)),-2(0.55-(5\theta_1+2\theta_2-12\theta_3)),-12(0.55-(5\theta_1+2\theta_2-12\theta_3)) \right \rangle$
理解梯度下降算法
用$\theta_0$代表起始点,想到到达附近的‘局部低点$\theta_1$’,公式如下
$\theta_1 = \theta_0 - \alpha \triangledown J(\theta)$
中间的减号-代表反方向,$\alpha$代表步长也称为学习率,$\triangledown J(\theta)$代表增速最快的方向。
α 步长
$\alpha$为每一次迭代的前进距离。
步幅大,前进速度快,但是容易越过最低点。
步幅小,不容易错过低点,但是用时更长。
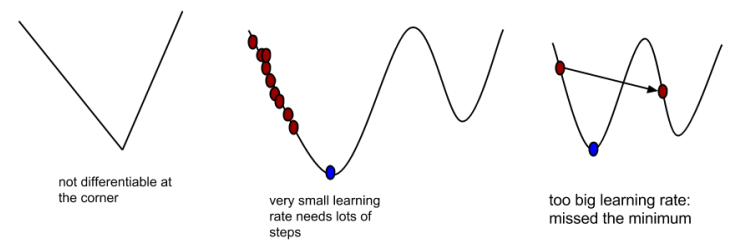
其中负号含义
梯度的正向是越来越高的,梯度下降,顾名思义,需要找到低点,所以应该向着梯度相反的方向前进。
一元函数例子
假设$J(\theta) = \theta^2$, 那么它的微分是$J'(\theta)=2\theta$,
假设起始点$\theta_0$=1,步长$\alpha$=0.4, 那么:
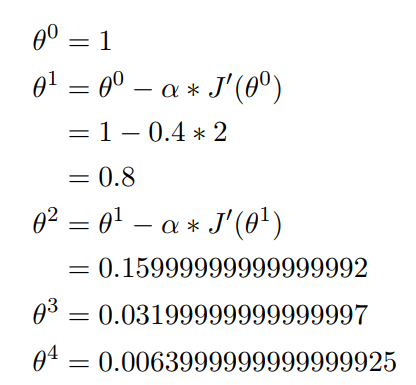
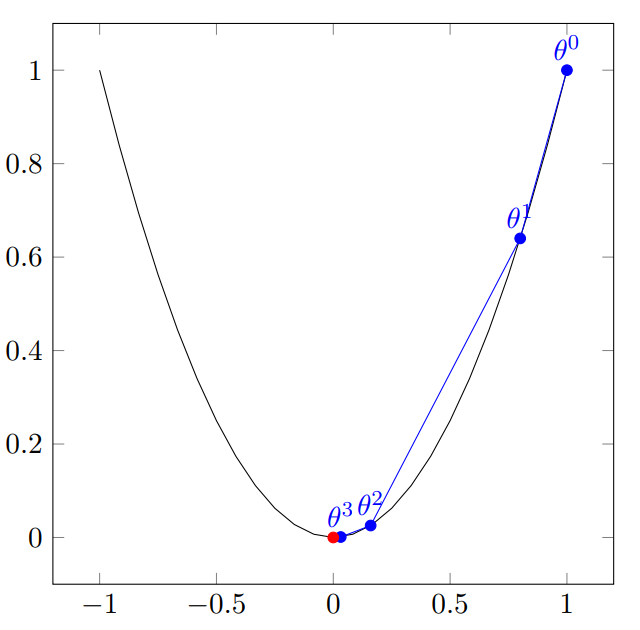
二元函数例子
假设$J(\theta)=\theta_1^2+\theta_2^2$,一看就知道(0,0)这个点是全局低点,那么我们试试用梯度下降能不能求出来:
假设$\theta_0$=(1, 3) 步长$\alpha$=0.1
它的梯度向量 $\triangledown J(\theta)= \left \langle 2\theta_1,2\theta_2 \right \rangle$
把$\theta_0$=(1, 3)代入梯度向量可得<2,6>

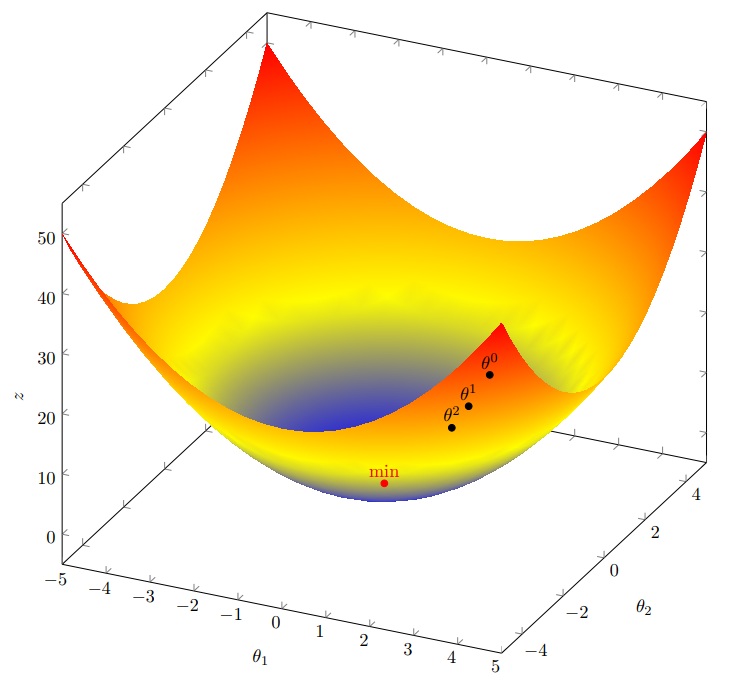
最终会越来越接近全局低点(0,0)

