概率无向图
定义
概率无向图模型(Probabilistic Undirected Graphical Model)是一个可以用无向图表示的联合概率分布。
它的整体结构是一张图(Graph),图中每一个节点表示一个或者一组变量,节点之间的边表示这两个/组变量之间的依赖关系。
概率无向图模型还有一个名字——马尔可夫随机场。
下图就是一个简单的马尔可夫随机场:
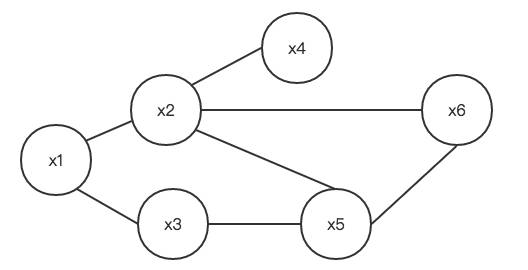
势函数和团
关于马尔可夫随机场,有几个非常重要的概念:
势函数(Potential Function,又称为因子 Factor):是定义在变量子集上的非负实函数,用于定义概率分布函数。
团(Clique):图中节点的子集,其中任意两个节点之间都有边连接。
极大团:一个团,其中加入任何一个其他的节点都不能再形成团。
马尔可夫随机场中,多个变量之间的联合概率分布可以基于团分解为多个势函数的乘积,每个势函数仅与一个团相关。
Hammersley-Clifford 定理
对于 $N$ 个变量的马尔可夫随机场,其变量为 $X=(X_1,X_2, …X_N) $(上图例子中 $N=6$)。
设所有团构成的集合为 $C$,与团 $Q \in C$ 对应的变量集合记作 $X_Q$,则联合概率为:
$P(X) = \frac{1}{Z}\prod_{Q \in C} \Psi_Q(X_Q)$
其中 $\Psi_Q$ 为与团 $Q$ 对应的势函数,用于对团 $Q$ 中的变量关系进行建模。
$Z$ 为规范化因子,很多时候要计算它很困难,不过好在大多数情况下,我们无须计算出 $Z$ 的精确值。
当团 $Q$ 不是极大团的时候,它必然属于某个极大团——实际上每一个非极大团都是如此,此时我们完全可以只用极大团来计算 $P(X)$:$P(X) = \frac{1}{Z^* } \prod_{Q \in C^* } \Psi_Q(X_Q)$,其中 $C^* $ 为所有极大团的集合。
这叫做 Hammersley-Clifford 定理,是随机场(Random Fields)的基础定理,它给出了一个马尔可夫随机场被表达为正概率分布的充分必要条件。
性质
在讨论马尔可夫随机场的性质之前,我们要学习两个概念。
两个概念
(1)分离(Separating)
设 $A,B,C$ 都是马尔可夫随机场中的节点集合,若从 $A$ 中的节点到 $B$ 中的节点都必须经过 $C$ 中的节点,则称 $A$ 和 $B$ 被 $C$ 分离,$C$ 称为分离集(Separating Set)。参加下图:
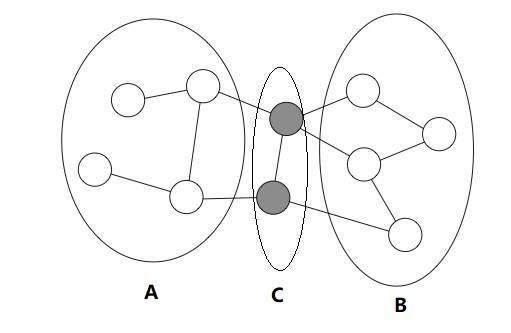
(2)马尔可夫性(Markov Property)
马尔可夫性的原始定义为:当一个随机过程在给定当前状态及所有过去状态情况下,其未来状态的条件概率分布仅依赖于当前状态;换句话说,在给定当前状态时,它与过去状态(即该过程的历史路径)是条件独立的,那么此随机过程即具有马尔可夫性。
我们把马尔可夫性引入到马尔可夫随机场中,把当前状态看作无向图中的一个节点,过去状态看作与当前状态节点有历史路径(边)连接的其他节点。
可以这样理解:在马尔可夫随机场的无向图中,任何一个节点的概率分布都仅和与它相连的节点有关。
形式化的表达为:设 $v$ 为无向图中任意一个节点,$W$ 是所有与 $v$ 相连的节点的集合,则 $v$ 的概率分布仅和 $W$ 有关,和 $v$ 与 $W$ 之外的其他节点无关 。
参看下图,给定灰色节点,则黑色节点独立于其他所有节点:

马尔可夫随机场的马尔可夫性
马尔可夫随机场具备全局马尔可夫性(Global Markov Property):给定两个变量子集的分离集,则这两个变量子集条件独立。
令 $A,B$ 和 $C$ 对应的变量集合分别为 $X_A,X_B, X_C$,则 $X_A$ 和 $X_B$ 在给定 $X_C$ 的条件下独立,记作:$X_A \perp X_B | X_C$。
即:$P(X_A, X_B|X_C) = P(X_A|X_C)P(X_B|X_C)$
由全局马尔可夫性,又可以推导出两种性质:
- 局部马尔可夫性(Local Markov Property):给定某变量的邻接变量,则该变量条件独立于其他变量。
用公式描述是:$P(X_v, X_O | X_W) = P(X_v|X_W)P(X_O|X_W)$,其中 $v$ 为无向图中任一节点,$W$ 是与 $v$ 有边连接的所有节点的集合,$O$ 是 $v$ 和 $W$ 之外的所有其他节点。
- 成对马尔可夫性(Pairwise Markov Property):给定所有其他变量,两个非连接变量条件独立。
公式描述为:$P(X_u, X_v | X_O) = P(X_u|X_O)P(X_v|X_O)$, 其中 $u$ 和 $v$ 为无向图中任意两个没有边连接的点,$O$ 为其他所有点的集合。
条件随机场(Conditional Random Field,CRF)
无向图模型
CRF 也是一种无向图模型。
它和马尔可夫随机场不同点在于:马尔可夫随机场是生成式模型,直接对联合分布进行建模;而条件随机场是判别式模型,对条件分布进行建模。
但两者又是相关的,CRF 是“有条件的”马尔可夫随机场。也就是说,CRF 是给定随机变量 $X$ 条件下,随机变量 $Y$ 的马尔可夫随机场。
定义
这里我们给出 CRF 的定义:设 $X$ 和 $Y$ 是随机变量,$P(Y|X)$ 是给定 $X$ 条件下 $Y$ 的条件概率分布。如果随机变量 $Y$ 构成一个由无向图 $G=<V, E>$ 表示的马尔可夫随机场,则称条件概率分布 $P(Y|X)$ 为 CRF。
换言之,设 $X$ 和 $Y$ 是随机变量,$P(Y|X)$ 是给定 $X$ 条件下 $Y$ 的条件概率分布。如果随机变量 $Y$ 构成一个无向图 $G=<V,E>$,且图 $G$ 中每一个变量 $Y_v$ 都满足马尔可夫性——$P(Y_v|X, Y_Z) = P(Y_v|X, Y_W) $,其中 $Z$ 表示无向图中节点 $v$ 以外所有点的集合,$W$ 表示无向图中与节点 $v$ 有边连接的所有节点集合——则 $P(Y|X)$ 为 CRF。
在 $P(Y|X)$ 中,$X$ 是输入变量,表示需要标注的观测序列;$Y$ 是输出变量,表示状态(或称标记)序列。
从定义层面,没有要求 $X$ 和 $Y$ 具有相同结构,不过在实际运行中,一般假设 $X$ 和 $Y$ 具备相同图结构。
线性链 CRF
在现实应用中,最常被用到的 CRF 是线性链(Linear Chain)CRF,其结构如下:
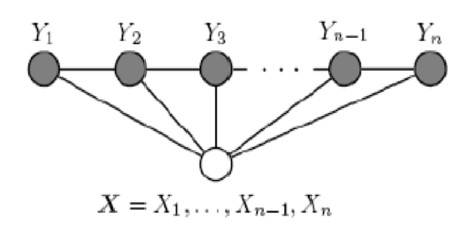
当 $X$ 和 $Y$ 具备相同结构时,其形如下:
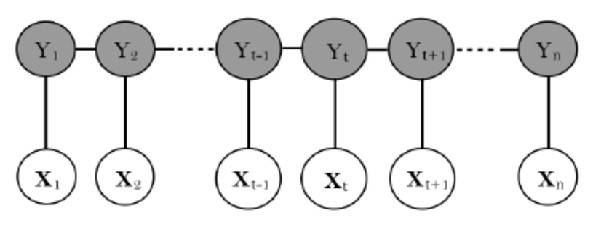
上图中,$X$ 为观测序列,$Y$ 为状态序列。
设 $X=(X_1,X_2, …, X_n)$,$Y = (Y_1, Y_2, …, Y_n)$,它们都是线性链表示的随机变量序列。
如果在给定随机变量序列 $X$ 的条件下,随机变量序列 $Y$ 的条件概率分布 $P(Y|X)$ 构成 CRF,也就是说它满足马尔可夫性:
$P(Y_i|X, Y_1, …, Y_{i-1}, Y_{i+1}, …, Y_n) = P(Y_i|X, Y_{i-1}, Y_{i+1})$
其中 $i=1,2,…, n$ (当 $i=1$ 和 $n$ 时只考虑单边),则称 $P(Y|X)$ 为线性链条件随机场。$X$ 为输入序列/观测序列,$Y$ 为输出序列/标记序列/状态序列。
HMM VS 线性链 CRF
看到此处是不是很眼熟,是不是又想到了 HMM?
确实,HMM 和 CRF 看起来蛮像的。
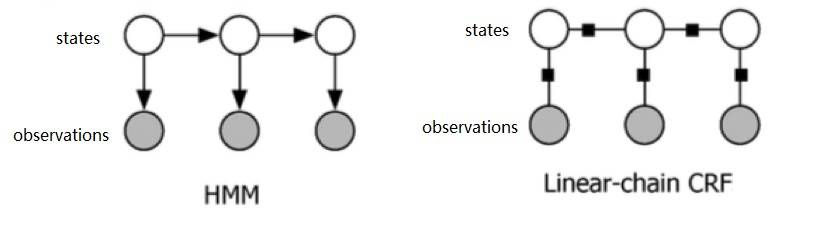
但是要注意:
- HMM 是有向图,CRF 是无向图;
- HMM 计算的是状态和观测的联合概率,而 CRF 计算的是状态基于观测的条件概率。
从使用的角度,HMM 多用于那种状态“原生”,而观测是状态“生成”出来的场景。
比如,用 HMM 来生成一段语音,则状态对应的是音节(声韵母)或文字,而观测则是这个音节所对应的声学特征。
这时,状态是相对客观的,观测是状态的一种“表征”,是状态“产生”出来的——我们想象一下自己说话时的场景,也是头脑中先想好说什么话,有了语言文字音节,然后再由大脑指挥喉舌发声。发出来的声音,就是最终的观测。
CRF 则多用于那种观测“原生”。状态“后天”产生,用来标记观测的情况。
比如,用 CRF 来做文本实体标记。输入一句话“我有一个苹果”,CRF 处理后将“苹果”标记成了“水果”。这个时候,“苹果”是观测,而“水果”则是对应的状态(或称标签)。
同一个观测值“苹果”,它的标签可以是“水果”,也可以是“手机”,具体是什么与训练数据有关,也与之前状态值有关。
但无论怎么样,观测才是客观存在的。而状态(标签)是人为“打”上去的,是以观测为条件进行“判别”的结果。
线性链 CRF 的形式化表示
一般形式
设 $P(Y|X)$ 为线性链 CRF,在随机变量 $X$ 取值为 $x$ 的条件下,随机变量 $Y$ 取值为 $y$ 的条件概率具有如下形式:
$P(y|x) =\frac{1}{Z(x)} \exp(\sum_{i,k} \lambda_k t_k (y_{i-1}, y_i, x, i) + \sum_{i,l}\mu_l s_l (y_i, x, i))$
其中,求和是在所有可能的输出序列上进行的。$t_k$ 和 $s_l$ 是特征函数,$\lambda_k$ 和 $\mu_l$ 是对应的权值——这四组参数确定了 CRF。
$t_k$ 是定义在(图模型的)边上的特征函数,称为转移特征,依赖当前和前一个位置。
$s_l$ 是定义在(图模型的)节点上的特征函数,称为状态特征,依赖于当前位置。
$t_k$ 和 $s_l$ 都是局部特征函数,因为它们都依赖于位置。通常的取值为$1$或者$0$。取值为$1$表示满足特征条件,否则为$0$。
$Z(x)$ 为规范化因子:
$Z(x) = \sum_{y} \exp(\sum_{i,k} \lambda_k t_k (y_{i-1}, y_i, x, i) + \sum_{i,l}\mu_l s_l (y_i, x, i))$
在实际使用中,当样本既定后,$Z(x)$ 也是既定的。
在这种情况下,$Z(x)$ 就可以被看作一个常数。因此:
$P(y|x) \propto \exp(\sum_{i,k} \lambda_k t_k (y_{i-1}, y_i, x, i) + \sum_{i,l}\mu_l s_l (y_i, x, i))$
用更清晰的表示,可写作:
$P(y|x) \propto \exp(\sum_{k=1}^{K} \lambda_k \sum_{i=1}^{n}t_k (y_{i-1}, y_i, x, i) + \sum_{l=1}^{L}\mu_l \sum_{i=1}^{n}s_l (y_i, x, i))$
上式表达的是,线性链 CRF 一共有 $K$ 个转移特征和 $L$ 个状态特征,它的观测序列和状态序列的长度为 $n$。它在 $X=x$ 条件下,$Y=y$ 的条件概率分布正比于经历如下步骤得出的内容:
- Step 1:将同一个特征(转移特征及状态特征)在各个位置求和,将局部特征转化为全局特征;
- Step 2:分别计算全局转移特征向量和全局状态特征向量与对应的权值向量的内积;
- Step 3:对 Step 2 的结果求 $exp(·)$。
简化形式
如果我们将转移特征和状态特征及其权值用统一的符号表示,线性链 CRF 形式化的表示就会简单许多。
设有 $K_1$ 个转移特征和 $K_2$ 个状态特征,且 $K=K_1 + K_2$。
我们用 $f_k(·)$ 来表示转移/状态特征函数:
$f_k(y_{i-1},y_i,x,i)= \begin{cases} \begin{array}{l}
t_k(y_{i-1},y_i,x,i),k=1,2...,K1 \\
sl(y_i,x,i), k=K_1+l,l=1,2,...,K_2
\end{array} \end{cases}(1)$
这样一来,在所有位置对转移/状态特征求和,就变成了:
$f_k(y,x) = \sum_{i=1}^{n}f_k(y_{i-1},y_i,x,i), \ \ k=1,2,..., K$
用 $w_k$ 表示特征 $f_k(y,x)$ 的权值,即
$w_k = \begin{cases} \begin{array}{l}
\lambda_k,k=1,2...,K1 \\
\mu_l, k=K_1+l,l=1,2,...,K_2
\end{array} \end{cases} (2)$
于是,线性链 CRF 的表示可以写作:
$P(y|x) = \frac{1}{Z(x)}\exp{\sum_{k=1}^{K}w_kf_k(y,x)}$
其中,$Z(x) = \sum_y\exp{\sum_{k=1}^{K}w_kf_k(y,x)}$。
设:
$w=(w_1, w_2, …, w_K)^T$ $F(y,x) =(f_1(y,x), f_2(y,x), …, f_K(y,x))^T$
则有:
$P_w(y|x) = \frac{\exp{(w·F(y,x))}}{Z_w(x)}$
其中,$Z_w(x) = \sum_y\exp{(w·F(y,x))}$。
注意:CRF 和马尔可夫随机场都是用团上的势函数来定义概率的。在表现形式上,二者非常接近。
但 CRF 处理的是条件概率,而马尔可夫随机场处理的是联合概率!
CRF 的三个基本问题
三个基本问题
类比于之前的 HMM,线性链 CRF 同样有三个基本问题。
1. 概率计算问题。
问题名称:概率计算问题。
已知信息:给定 CRF——
- $P(Y|X)$
- 观测序列 $x$
- 状态序列 $y$
求解目标:求条件概率 $P(Y_i = y_i|x)$, $P(Y_{i-1} = y_{i-1}, Y_i = y_i | x)$ 以及相应的数学期望。
2. 预测问题。
问题名称:预测问题。
已知信息:给定 CRF——
- $P(Y|X)$
- 观测序列 $x$
求解目标:求条件概率最大的状态序列 $y^* $,也就是对观测序列进行标注。
3. 学习问题
问题名称:学习问题。
已知信息:训练数据集。
求解目标:求 CRF 模型的参数。
对比 HMM 的三个基本问题
如果我们根据已知条件和求解目标来对比 CRF 和 HMM 的三个基本问题,则不难发现:它们在预测问题和学习问题上很类似。
对于预测问题,无论 HMM 还是 CRF 都是在模型已经存在(各个参数都已知)的情况下,给定观测序列,求最有可能与之对应的状态序列。
学习问题则都是在模型参数未知的时候,根据训练数据(观测序列)将模型的参数学习出来。
两者区别较大的是概率计算问题。
虽然在解决概率计算问题时,两者都已经有了既定的模型,但对于 HMM 而言,概率计算只需要观测序列即可,无须确定的状态序列,而最终计算出的结果,则是当前观测序列出现的可能性。
CRF 则需要既有已知观测序列,又有已知状态序列,这才能够去计算概率。
CRF 计算的是当前观测序列条件下,$i$ 节点对应的状态为 $y_i$ 的概率,或是当前观测序列条件下 $i$ 节点及其前面一个节点 $i-1$ 的状态分别为 $y_i$ 和 $y_{i-1}$ 的概率,或者是它们的数学期望。
三个基本问题的解法
鉴于 CRF 模型的具体算法较 HMM 难度更大,我们在此仅作简要说明。大家如果有兴趣,可以自行进一步研修。
概率计算问题
概率计算问题本身与 HMM 差别较大,但计算方法,却是借鉴了 HMM 的前向-后向算法,引入前向-后向向量,递归地计算每一步的概率。
我们将上面的 CRF 的简易形式化表达稍微该写一下:
$P(y|x) =\frac{1}{Z(x)} \exp(\sum_{k=1}^{K}\sum_{i=1}^{n} w_k f_k (y_{i-1}, y_i, x, i))$
其中:
$Z(x) = \sum_{y} \exp(\sum_{k=1}^{K}\sum_{i=1}^{n} w_k f_k (y_{i-1}, y_i, x, i))$
设:
$W_i(y_{i-1},y_i|x) = \sum_{k=1}^{K}w_k f_k(y_{i-1}, y_i, x, i)$
$M_i(y_{i-1},y_i|x) = \exp(W_i(y_{i-1},y_i|x)) $
令 $M_i(y_{i-1},y_i|x)$ 构成矩阵:$M_i(x) = [M_i(y_{i-1}, y_i|x)]$,$M_i(x)$ 是一个 $m$ 阶的矩阵($m$ 是状态 $y_i$ 取值的个数)。
状态序列原本有 $n$ 个节点,对应状态为 $(y_1, y_2, …, y_n)$。
这里,为了下面的计算,我们要引入一个起点,位置为 $0$,其状态为 $y_0$, 和一个终点,位置为 $n+1$ 其状态是 $y_{n+1}$。
于是有:
$P(y|x) = \frac{1}{Z(x)}\prod_{i=1}^{n+1} M_i(y_{i-1}, y_i, x, i)$
其中 $Z(x)$ 是 $n+1$ 个 $m \times m$ 矩阵的相乘之后的 $m \times m$ 矩阵中的一个元素的值,这个元素的行号对应的是 $y_0$ 所对应的状态序号,列号则是 $y_{n+1}$ 所对应的状态序号:
$Z(x) = (M_1(x)M_2(x)…M_{n+1}(x))_{y_0, y_{n+1}}$
有了以上这种表达方式之后,我们用前向-后向算法来解决 CRF 的概率计算问题,就容易多了。对每一个位置(包括起点和终点)$i=0,1,2,…, n, n+1$,定义前向向量:
$a_0(y|x) = \begin{cases} \begin{array}{lr}
1, & y=y_0 \\
0, & otherwise
\end{array} \end{cases}(3)$
$\alpha_i^T(y_i|x) = \alpha_{i-1}^T(y_{i-1}|x)M_i(y_{i-1},y_i|x), \ \ i =1,2,..., n+1$
并定义后向向量:
$\beta_{n+1}(y|x) = \begin{cases} \begin{array}{lr}
1,& y=y_{n+1} \\
0, & otherwise
\end{array} \end{cases}(4)$
$\beta_i(y_i|x) = M_i(y_i, y_{i+1} | x)\beta_{i-1}(y_{i+1}|x)$
根据前向向量和后向向量,推算出:
$P(Y_i=y_i|x) = \frac{\alpha_i^T(y_i|x)\beta_i(y_i|x)}{Z(x)}$
$P(Y_{i-1} = y_{i-1}, Y_i=y_i|x) = \frac{\alpha_{i-1}^T(y_{i-1}|x)M_i(y_{i-1},y_i|x)\beta_i(y_i|x)}{Z(x)}$
其中,$Z(x) = \alpha_n^T(x)\cdot \mathbf{1}$,$\mathbf{1}$ 是元素均为 $1$ 的 $m$ 维列向量。
预测问题
预测问题实际上是对观测序列进行标注。在给定的 CRF 之下,求给定观测序列最有可能对应的状态序列。
我们用 $x$ 表示观测序列,用 $y^* $ 表示最有可能的状态序列,则:
$y^* = max P(y|x) = max (\frac{1}{Z(x)}\exp{\sum_{k=1}^{K}w_kf_k(y,x)} ) $
因为 $Z(x)$ 是规范化因子,因此,实际上:
$ y^* \propto max (\exp{\sum_{k=1}^{K}w_kf_k(y,x)}) \propto max (\sum_{k=1}^{K}w_kf_k(y,x))$
最后问题变成了:$ max (\sum_{k=1}^{K}w_kf_k(y,x))$,也就是我们要找到使输出序列权值向量和特征向量内积最大的最优路径。
针对这一问题,可以和应对 HMM 的预测问题一样,采用维特比算法。
学习问题
线性链 CRF 模型实际上是定义在序列数据上的对数线形模型,可以通过极大化训练数据的对数似然函数来求模型参数。
训练数据的对数似然函数为:
$ L(w) = \sum_{i=1}^{n}\sum_{k=1}^{K}w_k f_k(y_i, x_i) - \sum_{i=1}^{n}\log{Z(x_i)}$
学习方法则有极大似然估计和正则化的极大似然估计。
具体的优化实现算法有:改进的迭代尺度法 IIS、梯度下降法以及拟牛顿法。目前应用较广的 BFGS 算法,属于拟牛顿法。
实例代码
在自然语言处理中,一个非常常见的任务就是从一个给定的句子或者段落中抽取出特定类型的词或短语。
比如判定实体名称(人名、地名、单位名等),或者是识别词性(名词、动词、形容词、副词等)。
这个问题叫做序列标注(sequance labeling),简单讲就是输入一个句子或段落,由识别模型给其中每一个词或短语打一个标签。
CRF模型的一个常见应用就是做这类识别模型。
这个实例是训练一个CRF模型,用它来识别文本中哪些词/短语属于一个名称(人名、地名、单位名等)。
如果这个词是一个名称的一部分就将其标识为“N”,否则标为“I”。
比如我们要判定这句话:"Paxar Corp said it has acquired Thermo-Print."
转换成输入: input = ["Paxar", "Corp", "said", "it", "has", "acquired", "Thermo-Print"]
再用CRF模型predict得到结果: output = ["N", "N", "I", "I", "I", "I", "N"]
module安装
pip install bs4
pip install nltk
pip install python-crfsuite
from bs4 import BeautifulSoup as bs
from bs4.element import Tag
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
import codecs
import nltk
import pycrfsuite
import numpy as np
# A function for extracting features in documents
def extract_features(doc):
return [word2features(doc, i) for i in range(len(doc))]
# A function fo generating the list of labels for each document
def get_labels(doc):
return [label for (token, postag, label) in doc]
def word2features(doc, i):
word = doc[i][0]
postag = doc[i][1]
# Common features for all words
features = [
'bias',
'word.lower=' + word.lower(),
'word[-3:]=' + word[-3:],
'word[-2:]=' + word[-2:],
'word.isupper=%s' % word.isupper(),
'word.istitle=%s' % word.istitle(),
'word.isdigit=%s' % word.isdigit(),
'postag=' + postag
]
# Features for words that are not
# at the beginning of a document
if i > 0:
word1 = doc[i-1][0]
postag1 = doc[i-1][1]
features.extend([
'-1:word.lower=' + word1.lower(),
'-1:word.istitle=%s' % word1.istitle(),
'-1:word.isupper=%s' % word1.isupper(),
'-1:word.isdigit=%s' % word1.isdigit(),
'-1:postag=' + postag1
])
else:
# Indicate that it is the 'beginning of a document'
features.append('BOS')
# Features for words that are not
# at the end of a document
if i < len(doc)-1:
word1 = doc[i+1][0]
postag1 = doc[i+1][1]
features.extend([
'+1:word.lower=' + word1.lower(),
'+1:word.istitle=%s' % word1.istitle(),
'+1:word.isupper=%s' % word1.isupper(),
'+1:word.isdigit=%s' % word1.isdigit(),
'+1:postag=' + postag1
])
else:
# Indicate that it is the 'end of a document'
features.append('EOS')
return features
# --- read data file, and parse xml ---
with codecs.open("reuters.xml", "r", "utf-8") as infile:
soup = bs(infile, "html5lib")
docs = []
for elem in soup.find_all("document"):
texts = []
# Loop through each child of the element under "textwithnamedentities"
for c in elem.find("textwithnamedentities").children:
if type(c) == Tag:
if c.name == "namedentityintext":
label = "N" # part of a named entity
else:
label = "I" # irrelevant word
for w in c.text.split(" "):
if len(w) > 0:
texts.append((w, label))
docs.append(texts)
data = []
for i, doc in enumerate(docs):
# Obtain the list of tokens in the document
tokens = [t for t, label in doc]
# Perform POS tagging
tagged = nltk.pos_tag(tokens)
# Take the word, POS tag, and its label
data.append([(w, pos, label) for (w, label), (word, pos) in zip(doc, tagged)])
# --- generate training/test data ---
X = [extract_features(doc) for doc in data]
y = [get_labels(doc) for doc in data]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# --- train ---
trainer = pycrfsuite.Trainer(verbose=True)
# Submit training data to the trainer
for xseq, yseq in zip(X_train, y_train):
trainer.append(xseq, yseq)
# Set the parameters of the model
trainer.set_params({
# coefficient for L1 penalty
'c1': 0.1,
# coefficient for L2 penalty
'c2': 0.01,
# maximum number of iterations
'max_iterations': 200,
# whether to include transitions that
# are possible, but not observed
'feature.possible_transitions': True
})
# Provide a file name as a parameter to the train function, such that
# the model will be saved to the file when training is finished
trainer.train('crf.model')
# --- predict/test ---
tagger = pycrfsuite.Tagger()
tagger.open('crf.model')
y_pred = [tagger.tag(xseq) for xseq in X_test]
# Let's take a look at a random sample in the testing set
i = 12
for x, y in zip(y_pred[i], [x[1].split("=")[1] for x in X_test[i]]):
print("%s (%s)" % (y, x))
# --- print test report ---
# Create a mapping of labels to indices
labels = {"N": 1, "I": 0}
# Convert the sequences of tags into a 1-dimensional array
predictions = np.array([labels[tag] for row in y_pred for tag in row])
truths = np.array([labels[tag] for row in y_test for tag in row])
# Print out the classification report
print(classification_report(
truths, predictions,
target_names=["I", "N"]))
还需要在py文件同目录下有这个文件resulter.xml
遇到nltk错误需要先进python,用nltk下载一点东西
python
>> import nltk
>> nltk.download('averaged_perceptron_tagger')

