最大期望算法EM

含有隐变量的概率模型

通过极大化对数似然函数求解概率模型参数

设有概率模型，${X}$ 表示其样本变量，$\Theta$ 表示其参数。

我们知道这个概率模型的形式，又有很多的样本数据（$X$ 取值已知），但是却不知道概率模型的具体参数值（$\Theta$ 取值未知）。有没有办法求出 $\Theta$ 的取值呢？

早在学习朴素贝叶斯模型的时候，我们就知道：当一个概率模型参数未知，但有一系列样本数据时，可以采用极大似然估计法来估计它的参数。

该概率模型的学习目标是极大化其对数似然函数：

$LL(\Theta|X) = \log{P(X | \Theta)}$

此时，根据 $X$ 直接极大化 $LL(\Theta|X) $ 来求 $\Theta$ 的最优取值即可。

此处的 $X$ 必须是完全数据——也就是样本数据所有变量的值都是可见且完整的情况下，才可以通过直接极大化对数似然函数来求解参数的值。

含有隐变量的对数似然函数

有的时候，概率模型既含有可以看得见取值的观测变量，又含有直接看不到的隐变量（Hidden Variable，又称潜在变量 Latent Variable）。

设有概率模型，${X}$ 表示其观测变量集合，$Z$ 表示其隐变量集合，$\Theta$ 表示该模型参数。

注意：$ {X}$ 和 $Z$ 合在一起被称为完全数据（Complete-data），仅有 $X$ 称为不完全数据（Incomplete-data）。

要对 $\Theta$ 进行极大似然估计，就是要极大化 $\Theta$ 相对于完全数据的对数似然函数——隐变量 $Z$ 存在时的对数似然函数为：

$LL(\Theta|X,Z) = \log{P(X,Z | \Theta)}$

我们无法通过观测获得隐变量的取值，样本数据不完全。这种情况下，直接用极大似然估计，就不行了。只好请 EM 算法出马。

EM 算法基本思想

EM（期望最大化，Expectation-Maximization）算法，是一种用于对含有隐变量的概率模型的参数，进行极大似然估计的迭代算法。

近似极大化

EM 算法的基本思想是：近似极大化——通过迭代来逐步近似极大化。

我们有一个目标函数：$\arg{\max{f(\theta)}}$。

然而，由于种种原因，我们对于当前这个要求取极大值的函数本身的形态并不清楚，因此无法通过诸如求导函数并令其为零（梯度下降）等方法来直接探索目标函数极大值。也就是不能直接优化 $f(\theta)$！

但是我们可以采用一个近似的方法。

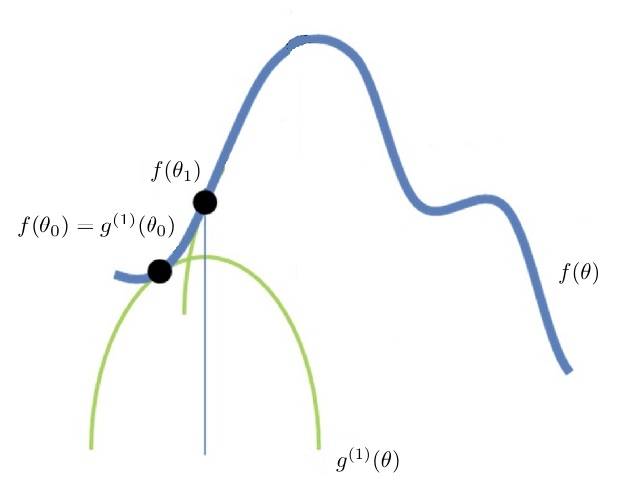
首先构建一个我们确定可以极大化的函数 $g^{(1)}(\theta)$，并且确保：

$f(\theta) \geqslant g^{(1)}(\theta) $；
存在一个点 $\theta_0$，$f(\theta_0)$ 和 $g^{(1)}(\theta_0)$ 在 $\theta_0$ 点相交，即：$f(\theta_0) = g^{(1)}(\theta_0)$；
$\theta_0$ 不是 $g^{(1)}(\theta) $ 的极大值点。

在这种情况下，我们极大化 $g^{(1)}(\theta)$，得到 $g^{(1)}(\theta)$ 的极大值点 $\theta_1$，即：$\max{ g^{(1)}(\theta)} = g^{(1)}(\theta_1)$。

由1、2和3可知，$g^{(1)}(\theta_1) > g^{(1)}(\theta_0) => f(\theta_1) > f(\theta_0)$。

可见，极大化 $g^{(1)}(\theta)$ 的过程，就相当于沿着 $\theta$ 方向，向着 $f(\theta)$ 的极大值前进了一步（见图1）。

图 1

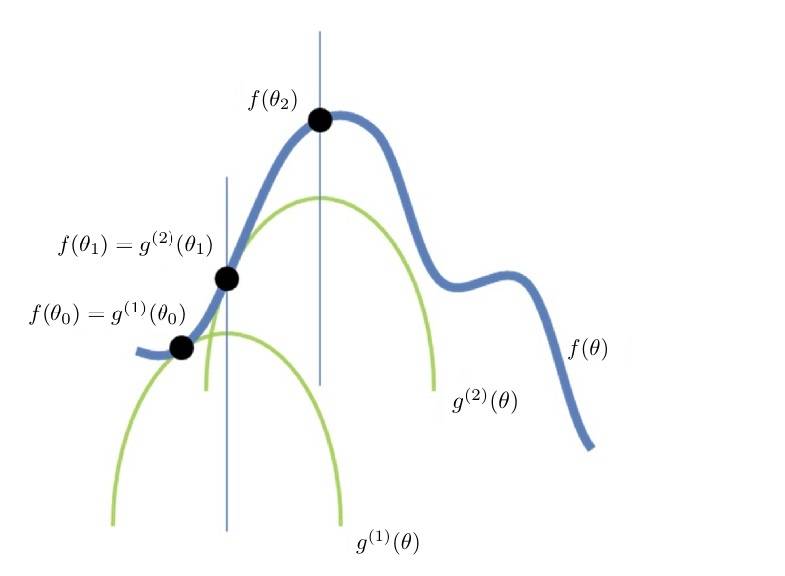
然后，再构建一个函数 $g^{(2)}(\theta)$，使得：

$f(\theta) \geqslant g^{(2)}(\theta) $;
$f(\theta_1) = g^{(2)}(\theta_1)$；
$\theta_1$不是$g^{(2)}(\theta)$的极大值点。

接着极大化 $g^{(2)}(\theta)$，得到 $g^{(2)}(\theta)$ 的极大值点 $\theta_2$，于是：$f(\theta_2) > f(\theta_1)$，$f(\theta)$又朝着自身极大化前进了一步。（见图2）

图 2

我们不断重复上述的过程，一次又一次。每一次分别构建出函数：$g^{(1)}(\theta)$, $g^{(2)}(\theta)$, ..., $g^{(m-1)}(\theta)$, $g^{(m)}(\theta)$。

直到过程收敛——新创建出来的函数 $g^{(m)}$ 的极大值和 $g^{(m-1)}$ 的极大值几无差别为止。

这个时候，我们就取 $g^{(m)}(\theta)$ 的极大值作为 $f(\theta)$ 的极大值，虽然可能还不是 $f(\theta)$ 事实上的极大值，但是也已经非常近似了。

真正的目标

要知道，整个算法的目的是用近似法估计参数 $\theta$，我们真正的目标是：求出让 $f(\theta)$ 达到近似极大值的 $\theta^* $；而不是去求 $f(\theta^* )$ 或是逼近它的 $g^{(m)}(\theta^* )$ 本身的值！

实际上，如果我们有办法能够一步步推进 $\theta$ 的取值，先求出 $\theta_1$ 再求出 $\theta_2$、$\theta_3$…… 一直到让 $g^{(m)}(\theta)$ 达到极大值的 $\theta^* $ ——只要求出 $\theta^* $，也就达到目的了。

而其间用来逐步推进的 $g^{(1)}(\theta)$, $g^{(2)}(\theta)$, ... , $g^{(m)}(\theta)$ 等函数的具体形式到底是什么，我们其实并不关心。

这么说到底是什么意思呢？别急，到下一小节你就明白了。

EM 算法的推导过程

上面我们详细讲解了 EM 算法的原理，那么原理又如何对应到求概率模型的参数呢？

优化目标

我们不妨这样来看。

概率模型参数估计问题的目标是极大化对数似然函数：$LL(\Theta|X) = \log{P(X | \Theta)}$。

我们要找到一个具体的 $\Theta^* $，将这个 $\Theta^* $ 带入到对数似然函数后，在当前所有样本观测数据 $X$ 的前提之下，使得对数似然函数达到极大值。

这里比较麻烦的是 $X$ 不是完全数据而只是观测变量，我们还有个隐变量 $Z$。

将观测数据表示为 $X = (X_1, X_2, ..., X_n)^T$，隐变量表示为 $Z = (Z_1, Z_2, ..., Z_n)^T$，则观测数据的似然函数为 $P(X|\Theta) = \sum_Z P(X|Z,\Theta)P(Z|\Theta) $。

注意：此处需要运用一个计算技巧：通过对隐变量 $Z$ 进行求积分（或求和）操作，来将其转化为观测变量的“边际似然”（Marginal Likelihood）。

故而：

$LL(\Theta|X) = \log{P(X | \Theta)} = \log{ \sum_Z P(X|Z,\Theta) P(Z|\Theta) }$

因为其中的 $Z$ 是不可见的（未知的），所以我们无法直接最优化 $LL(\Theta|X)$。

应用 EM 算法

无法直接最优化目标，那就按我们刚才介绍的方法来做近似最优化吧。

此处，$LL(\Theta|X)$ 就相当于原理中的 $f(\theta)$。我们只需要找到对应的 $g^{(t)}(\theta)$ 就可以运用 EM 算法啦（这里的 $t$ 表示时刻，也可以理解为迭代的序号）！

我们知道，EM 是一个迭代算法，每一次迭代结果会估计出一个新的参数值 $\Theta^{t}$，相应地也就可以求出 $LL(\Theta^{t}|X)$。

我们希望的是每一次的迭代都能让 $LL(\Theta|X)$ 取值增加，那么自然，其中具体一次迭代的结果必然比函数本身的极大值要小。也就是有 $LL(\Theta|X) > LL(\Theta^{t}|X)$。

注意：此处的 $\Theta^{t}$ 是上一个迭代算出来的确定结果，对于当前迭代，是一个已知的定值。

此处的 $\Theta$ 还是一个未知的值，是我们要求取的能够让 $LL(\Theta|X)$ 达到极大值的参数。

为了达到 $LL(\Theta|X) > LL(\Theta^{t}|X)$ 的效果，我们当然需要想办法使得 $LL(\Theta|X) - LL(\Theta^{t}|X) > 0$。

于是就要先来计算：

$LL(\Theta|X) - LL(\Theta^{t}|X) $

$= \log\sum_Z {P(X|Z,\Theta)P(Z|\Theta)} - \log{ P(X|\Theta^{t})} $

$= \log\sum_Z P(Z|X, \Theta^{t})\frac{P(X|Z,\Theta)P(Z|\Theta)}{P(Z|X, \Theta^{t})} - \log{ P(X|\Theta^{t})} $

在这里我们运用詹森不等式（Jensen's inequality）有：

$LL(\Theta|X) - LL(\Theta^{t}|X) \geqslant \sum_Z {P(Z|X, \Theta^{t})\log \frac{P(X|Z,\Theta)P(Z|\Theta)}{P(Z|X, \Theta^{t})}} - \log{ P(X|\Theta^{t})}$

其中 $\sum_Z P(Z|X, \Theta^{t}) = 1$。

詹森不等式：对于一个凸函数，函数的积分大于等于积分的函数。

形式化表示为：$\log{\sum_j \lambda_j x_j} \geqslant \sum_j{\lambda_j}\log{x_j}$, 其中 $\lambda_j \geqslant 0 , \sum_j \lambda_j = 1$。

不等式的右侧：

$\sum_Z {P(Z|X, \Theta^{t})\log \frac{P(X|Z,\Theta)P(Z|\Theta)}{P(Z|X, \Theta^{t})}} - \log{ P(X|\Theta^{t})} = \sum_Z P(Z|X, \Theta^{t})\log \frac{P(X|Z,\Theta)P(Z|\Theta)}{P(Z|X, \Theta^{t})P(X|\Theta^{t})}$

令：

$l(\Theta, \Theta^{t}) = LL(\Theta^{t} |X) + \sum_Z P(Z|X, \Theta^{t})\log \frac{P(X|Z,\Theta)P(Z|\Theta)}{P(Z|X, \Theta^{t})P(X|\Theta^{t})}$

则有：

$LL(\Theta|X) \geqslant l(\Theta, \Theta^{t})$，并且 $ LL(\Theta^{t}|X) = l(\Theta^{t}, \Theta^{t})$。

$LL(\Theta|X)$ 相当于原理中的 $f(\theta)$，而 $l(\Theta, \Theta^{t})$ 则相当于 $g^{(t)}(\theta)$。

这两者关系可视化在二维坐标中，就像下图3这样（类比一下“原理”一节中的蓝、绿两条曲线）：

图 3

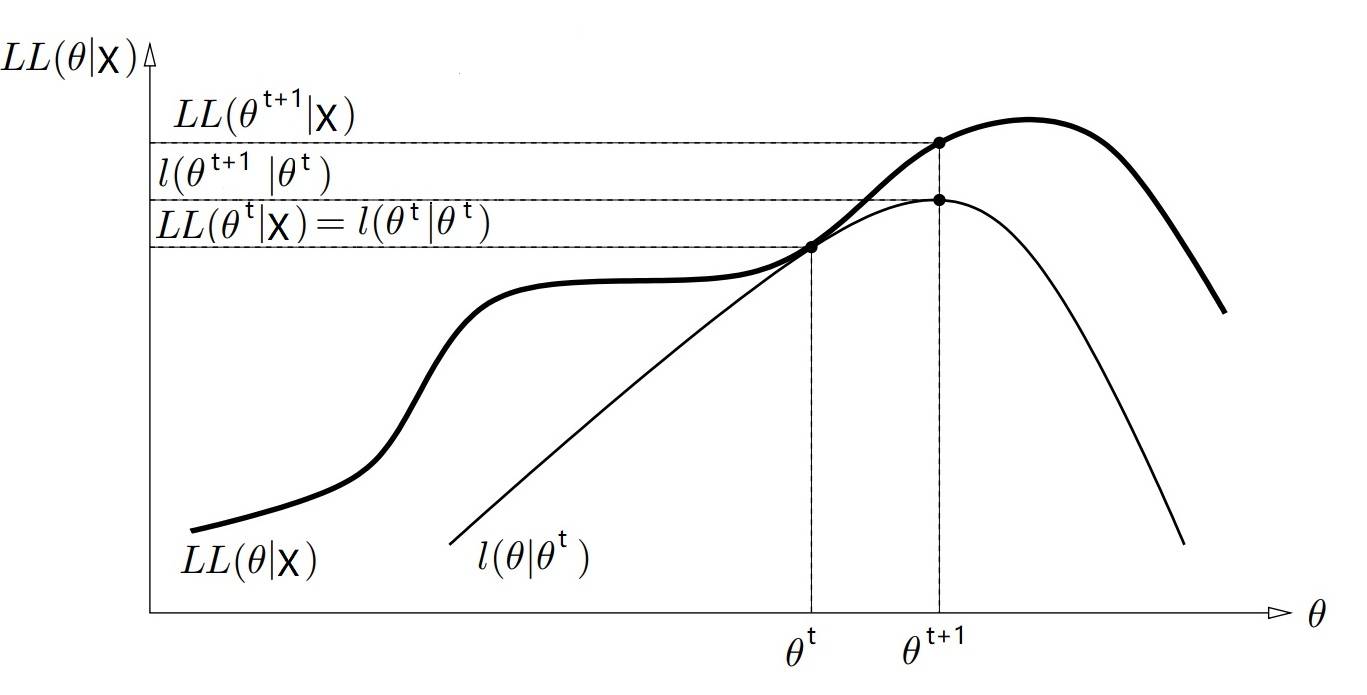
那么自然 $\Theta^{t}$ 就是本次迭代中原目标函数与近似函数相交的交点：$ LL(\Theta^{t}|X) = l(\Theta^{t}, \Theta^{t}) $（此处请类比：$ f(\theta_t) = g^{(t)}(\theta_t) $，想想图1里的 $\theta_0$）。

而 $\Theta^{t+1}$ 则是使得本次迭代的近似函数 $ l(\Theta, \Theta^{t})$ 达到极大值的参数（想想图1中的 $\theta_1$）。

又因为：

$\Theta^{t+1} =\arg{ \max_{\Theta}{ l(\Theta, \Theta^{t})}} \\
= \arg{\max{[ LL(\Theta^{t} |X) + \sum_Z P(Z|X, \Theta^{t})\log \frac{P(X|Z,\Theta)P(Z|\Theta)}{P(Z|X, \Theta^{t})P(X|\Theta^{t})} ]}} \\
= \arg{\max{[\sum_Z (P(Z|X, \Theta^{t})\log \frac{P(X|Z,\Theta)P(Z|\Theta)}{P(Z|X, \Theta^{t})} ]}} \\
=\arg{\max{[\sum_Z (P(Z|X, \Theta^{t})(\log P(X|Z,\Theta)P(Z|\Theta) - \log{P(Z|X, \Theta^{t})}))]}}$

要知道，上式是在优化 $\Theta$，而其中的 $ \log{P(Z|X, \Theta^{t})}$ 和 $\Theta$ 的优化无关，所以可以直接不去管它。

因此：

$ \arg{\max_{\Theta}{ l(\Theta, \Theta^{t})}} \\
= \arg{\max{[\sum_Z P(Z|X, \Theta^{t})\log P(X|Z,\Theta)P(Z|\Theta)]}} \\
= \arg{\max{[\sum_Z P(Z|X, \Theta^{t})\log P(X,Z|\Theta)]}}$

设：

$Q(\Theta,\Theta^t) = \sum_Z P(Z|X, \Theta^{t})\log P(X,Z|\Theta)$。

那么只要求出使得函数 $Q(\Theta,\Theta^t)$ 极大化的 $\Theta$，就是 $\Theta^{t+1}$ 了，它同时也是下一次迭代的近似函数和目标函数的交点。

则，在 EM 算法的每一次迭代中，我们只需要：

先求 $Q(\Theta,\Theta^t)$；
再求使得 $Q(\Theta,\Theta^t)$ 极大化的 $\Theta^{t+1}$，确定下一次迭代的参数估计值。

这样就可以了！

第一次迭代的初始参数估计 $\Theta^0$ 可以人工选取，此后的每次迭代都如此这般，一次次迭代下来，就可以通过近似极大化的方法得出我们的参数估计结果了！

EM 算法步骤

前面我们讲了 EM 算法的基本原理和推导，现在我们来看看它的具体过程。

Step 1：选择参数的初始值 $\Theta^0$，作为起点开始迭代。

理论上，$\Theta^0$ 值可以任意选择，不过 EM 算法对于初值敏感，如果初值选择不当可能会影响算法效率甚至最终的结果。

Step 2：E 步。

E 的含义是：期望（Expectation）。

在 E 步，我们要做的就是求出 $Q(\Theta,\Theta^t)$。

$\Theta^t$ 为上一次迭代时 M 步（Step 3）得出的参数估计结果（第一次迭代时 $\Theta^t$ 等于初值 $\Theta^0$），在此次迭代的本步中，我们要计算 $Q$ 函数：

$Q(\Theta,\Theta^t)= \sum_Z P(Z|X, \Theta^t) \log{P(X,Z|\Theta)} $

其中 $P(Z|X, \Theta^t)$ 是在给定观测数据 $X$ 和当前的参数估计 $\Theta^t$ 下，隐变量数据 $Z$ 的条件概率分布。

因为：

$\sum_Z P(Z|X, \Theta^t) \log{P(X,Z|\Theta)} = E_{Z | X, \Theta^t}[\log{P(X,Z|\Theta)}] = E_{Z | X, \Theta^t}LL(\Theta|X,Z) $

所以说，E 步计算的是：完全数据的对数似然函数 $LL(\Theta|X,Z)$，在给定观测数据 $X$ 和当前参数 $\Theta^t$ 下，对于未观测数据 $Z$ 的期望。

因为 $\Theta^t$ 在此时是已知的，且 $X$ 原本就是已知的，故而可以根据训练数据推断出隐变量 $Z$ 的期望，记作 $E^{(t)}(Z)$。

而 $Q(\Theta,\Theta^t)= E_{Z | X, \Theta^t}LL(\Theta|X,Z) $ 本来是一个含有变量 $\Theta$ 和 $Z$ 的函数，我们能将它转换成含有变量 $\Theta$ 和 $E^{(t)}(Z)$ 的函数形式：

$Q(\Theta,\Theta^t) = R(\Theta, E^{(t)}(Z))$

再将刚刚得出的 $E^{(t)}(Z)$ 带入其中，就将其转变成了关于 $\Theta$ 的函数：

$Q(\Theta,\Theta^t) = R(\Theta, E^{(t)}(Z)) = R^{(t)}(\Theta)$

Step 3：M步。

M 的含义是：最大化（Maximization）。

在 M 步，我们要求的是使得 $Q(\Theta,\Theta^t)$ 极大化的 $\Theta$，也就是下一次迭代的参数估计值：

$\Theta^{t+1} = \arg{\max_\Theta {Q(\Theta, \Theta^t)}}$

因为上面 E 步已经成功将 $Q(\Theta, \Theta^t)$ 转化成了一个仅含有 $\Theta$ 变量的函数 $R^{(t)}(\Theta)$，那么本步自然可以方便地对参数 $\Theta$ 做极大似然估计了。

**Step 4：**迭代执行 E-M 两步，直至收敛。

每一次 E-M 迭代都使得对数似然函数增大。这样一轮轮地迭代下来，直至收敛——收敛的条件如下：

存在非常小的两个正数 $\epsilon_1$ 和 $\epsilon_2$，若满足

$||\Theta^{t+1} - \Theta^t|| < \epsilon_1$ 或者 $|| Q(\Theta^{t+1}, \Theta^{t}) - Q(\Theta^{t}, \Theta^{t})|| < \epsilon_2$

则停止迭代。

因为整个算法中最关键的是 E 步和 M 步，所以这个算法称为 EM 算法