增长率
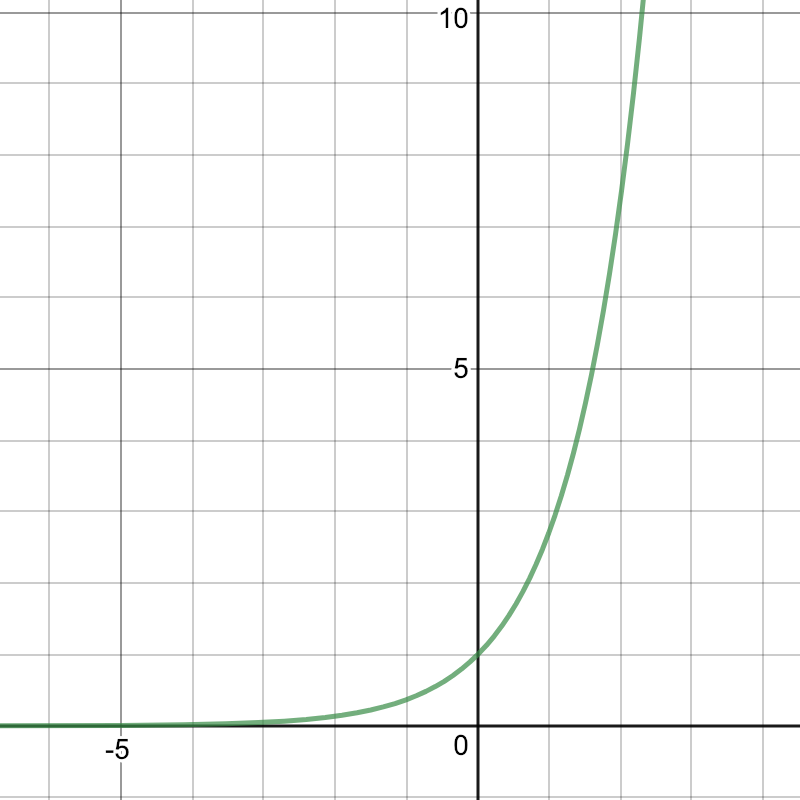
指数函数 $f(x) = e^{x}$ 的微分函数还是 $e^{x}$。因此,很自然地,将指数函数引入其中,则有:
$W(t) = be^{wt}$
图像成以下分布:
逻辑函数
在自然界中,当一种东西数量越来越多以后,某种阻力也会越来越明显地抑制其增长率
新的模型:$W'(t) = wW(t)(1-\frac{W(t)}{L})$
$L$ 表示 $W(t)$ 的上限
设:$P(t) = \frac{W(t)}{L}$
则有:$P'(t) = wP(t)(1 – P(t))$
上式是一个一阶自治微分方程(Autonomous Differential Equations),我们求解这个微分方程,得出:
$P(t) = \frac{e^{(wt+b)}}{ 1 + e^{(wt+b)}}$
图像成这样的分布:
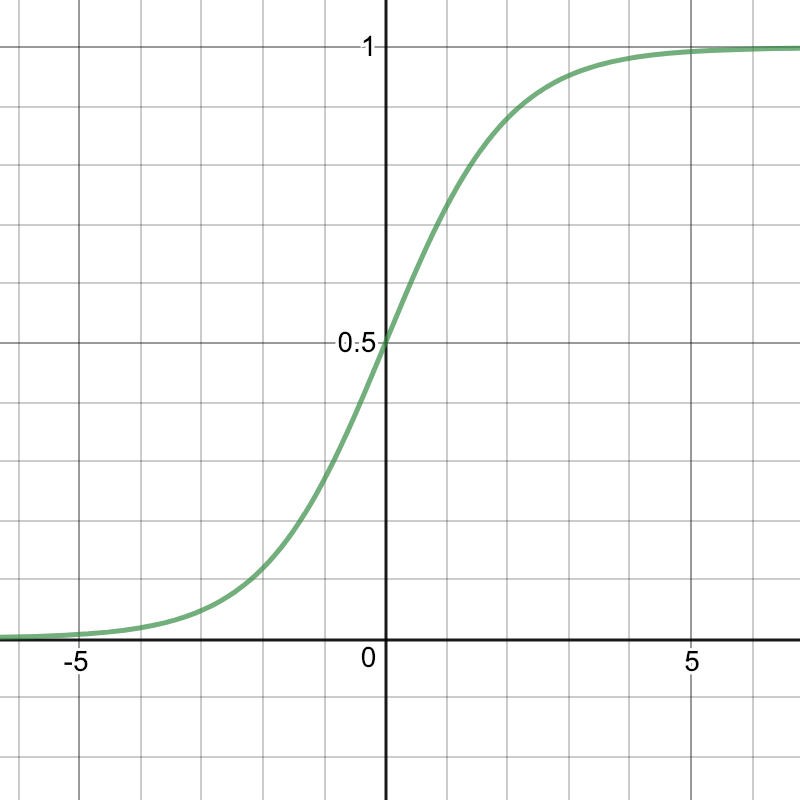
也就是 Sigmoid函数:
$P(t) = \frac{1}{1 + e^{-(wt+b)}}$
将 $t$ 替换为 $x$,$P$ 替换为 $h$ 就是:
$h(x) = \frac{1}{1 + e^{-(wx+b) }} $
当 $x$ 为多维时,$wx+b$ 用两个向量相乘 $\theta^T x$ 表示,
$h_\theta(x) = \frac{1}{1 + e^{-\theta^Tx }} $
逻辑回归函数对比线性回归函数
$\theta = w,b$
逻辑回归函数:
$f_{w,b}(x) = h_\theta (\sum_iw_ix_i+b)$
output: 0~1
线性回归函数:
$f_{w,b}(x) = \sum_iw_ix_i+b$
output: 任何值
回归模型做分类
设 $z = \theta^T x$,则
$h(z) = \frac{1}{1 + e^{-z }} $
逻辑回归的目标函数
$P(y=1|x) = h(x); P(y=0|x) = 1- h(x)$
根据二项分布公式,可得出 $P(y|x) = h(x) ^y(1- h(x))^{(1-y)}$
假设我们的训练集一共有 m 个数据,那么这 m 个数据的联合概率就是:
$L(\theta) = \prod_{i=1}^{m}P(y^{(i)}|x^{(i)};\theta) $
$= \prod_{i=1}^{m}(h_\theta(x^{(i)}))^{y^{(i)}}(1-h_\theta(x^{(i)}))^{(1-y^{(i)})}$
求取 $\theta$ 的结果,就是让这个 $L(\theta)$ 达到最大
现有data set:
| $x_1$ | $x_2$ | $x_3$ | ... | $x_n$ |
|---|---|---|---|---|
| $C_1$ | $C_1$ | $C_2$ | ... | $C_1$ |
$L(\theta) = h_{\theta}(x_1)h_{\theta}(x_2)(1-h_{\theta}(x_3))...h_{\theta}(x_n)$
$\theta^* =arg\ \underset{\theta}{max}\ L(\theta)$
也就是 $\theta^* =arg\ \underset{\theta}{min}-logL(\theta)$
$-logL(\theta)$
$= -log\ h_{\theta}(x_1)) = -[\hat{y_1}\ log\ h(x_1) + (1-\hat{y_1})log(1-f(x_1))]$
$-log\ h_{\theta}(x_2)) = -[\hat{y_2}\ log\ h(x_2) + (1-\hat{y_2})log(1-f(x_2))]$
$-log(1-\ h_{\theta}(x_3))) = -[\hat{y_3}\ log\ h(x_3) + (1-\hat{y_3})log(1-f(x_3))]$
...
设 $\hat{y_1}=C_1=1$,$\hat{y_2}=C_1=1$,$\hat{y_3}=C_2=0$ ...
代入 $\hat{y_1}=1$,$\hat{y_2}=1$,$\hat{y_3}=0$...
$=-\log\ h(x_1) - \log\ h(x_2) - log(1-h(x_3))...$
以上可推导出:
$= \sum_{i=1}^{n}-[y^{(i)}\log(h_\theta(x^{(i)})) + (1-y^{(i)})\log(1-h_\theta(x^{(i)}))]$
这条式子相当于我们对$L(\theta)$求对数的相反数, 即负对数似然函数:
$-l(\theta) = -\log(L(\theta)) $
去除负号可得到对数似然函数:
$l(\theta) = \log(L(\theta)) $
这是一个凸函数,具备最小值,因此$l(\theta)$ 可以作为 LR 的目标函数。所以我们设定:$J(\theta) = -l(\theta) $
$J(\theta) = - \log(L(\theta)) $
$= -\sum_{i=1}^{m}[y^{(i)}\log(h_\theta(x^{(i)})) + (1-y^{(i)})\log(1-h_\theta(x^{(i)}))]$
$J(\theta)$ 就是 LR 的目标函数
这个其实是两个伯努利分布(Bernoulli distribution)的交叉熵(Cross entropy)。
p分布
$p(x=1)=\hat{y_n}$
$p(x=0)=1-\hat{y_n}$
q分布
$q(x=1)=f(x^n)$
$q(x=0)=1-f(x^n)$
$H(p,q)=-\sum_x p(x)ln(q(x))$
这公式其实是在对比两个分布之间有多接近。
优化算法
LR 的目标函数 $J(\theta)$,优化的目标是最小化它。
最常见最基础的梯度下降算法,基本步骤如下:
- 通过对 $J(\theta)$ 求导获得下降方向 $J'(\theta) $;
- 根据预设的步长 $\alpha$,更新参数 $\theta$,$\theta − \alpha J’(θ)$;
- 重复以上两步直到逼近最优值,满足终止条件。
已知:
$J(\theta) = - \log(L(\theta)) = -\sum_{i=1}^{m}[y^{(i)}\log(h_\theta(x^{(i)})) + (1-y^{(i)})\log(1-h_\theta(x^{(i)}))]$
$J(\theta)$ 对 $\theta$ 求导 $\frac{\partial{ J(\theta)}}{\partial{\theta}} $:
左边的 $\frac{\partial \log(h_\theta(x^{(i)})}{\partial \theta} = \frac{\partial \log(h_\theta(x^{(i)})}{\partial z} \frac{\partial z}{\partial w_i}$
$\because z = wx+b=\sum_{i}^{}w_ix_i+b$
$\therefore \frac{\partial z}{\partial w_i} = x_i$
设 $h_\theta (x^{(i)}) = \sigma (z) = \frac{1}{1+e^{-z}}$
$\frac{\partial \log(h_\theta(x^{(i)})}{\partial z} = \frac{\partial \log(\sigma (z))}{\partial z} = \frac{1}{\sigma (z)} \frac{\partial \sigma (z)}{\partial z}$
$\because \frac{\partial \sigma (z)}{\partial z} = \frac{\partial(\frac{1}{1+e^{-z}})}{\partial z} $
$= -(\frac{-e^{-z}}{(1 + e^{-z})^2}) = \frac{e^{-z}}{1+e^{-z}}\frac{1}{1+e^{-z}} $
$= (1- \frac{1}{1+e^{-z}})(\frac{1}{1+e^{-z}} ) = \sigma(z)(1 - \sigma(z))$
$\therefore =\frac{1}{\sigma (z)}\sigma (z)(1-\sigma (z))$
$=1-\sigma (z)$
$\therefore \frac{\partial \log(h_\theta(x^{(i)})}{\partial \theta} = (1-h_\theta (x^{(i)}))x^{(i)}$
右边的 $\frac{\partial \log(1-h_\theta(x^{(i)})}{\partial z} = \frac{\partial \log(1-\sigma (z)}{\partial z} = \frac{1}{1-\sigma (z)} \frac{\partial \sigma (z)}{\partial z}$
$\frac{1}{1-\sigma (z)}\sigma (z)(1-\sigma (z)) = \sigma (z)$
将上式带入上面的 $J(\theta)$ 求导式子里,有:
$\frac{\partial{J(\theta)}}{\partial{\theta}}$
$=\sum_{i=1}^{m}[(-y^{(i)})(1- h_\theta(x^{(i)}))x^{(i)} + (1-y^{(i)})h_\theta(x^{(i)})x^{(i)}]$
$=\sum_{i=1}^{m}[-y^{(i)} + y^{(i)}h_\theta(x^{(i)}) + h_\theta(x^{(i)}) - y^{(i)}h_\theta(x^{(i)}) ]x^{(i)} $
$=\sum_{i=1}^{m}[ h_\theta(x^{(i)}) -y^{(i)}]x^{(i)}$
当 $x$ 为多维的时候(设 $x$ 有 $n$ 维),则在对 $z=\theta x$ 求导的时候,要对 $x$ 的每一个维度求导。
又因为 $\theta$ 和 $x$ 维度相同,所以当 $x$ 有 $n$ 维的时候,$\theta$ 同样是有 $n$ 维的。
则 $J(\theta)$ 的求导也变成了对 $\theta$ 的每一个维度求导:
$\frac{\partial{ J(\theta)}}{\partial{\theta_j}} $
$=\sum_{i=1}^{m}[ h_\theta(x^{(i)}) -y^{(i)}]x_j^{(i)} ;\quad j = 1, 2, ..., n$
实例及代码实现
from sklearn.linear_model import LogisticRegression
from sklearn.linear_model import LinearRegression
import pandas as pd
# Importing dataset
data = pd.read_csv('quiz.csv', delimiter=',')
used_features = [ "Last Score", "Hours Spent"]
X = data[used_features].values
scores = data["Score"].values
X_train = X[:11]
X_test = X[11:]
# Logistic Regression – Binary Classification
passed = []
for i in range(len(scores)):
if(scores[i] >= 60):
passed.append(1)
else:
passed.append(0)
y_train = passed[:11]
y_test = passed[11:]
classifier = LogisticRegression(C=1e5)
classifier.fit(X_train, y_train)
y_predict = classifier.predict(X_test)
print(y_predict)
quiz.csv
Id,Last Score,Hours Spent,Score
1,90,117,89
2,85,109,78
3,75,113,82
4,98,20,95
5,62,116,61
6,36,34,32
7,87,120,88
8,89,132,92
9,60,83,52
10,72,92,65
11,73,112,71
12,56,143,62
13,57,97,52
14,91,119,93
LR 处理多分类问题
from sklearn.linear_model import LogisticRegression
from sklearn.linear_model import LinearRegression
import pandas as pd
# Importing dataset
data = pd.read_csv('quiz.csv', delimiter=',')
used_features = [ "Last Score", "Hours Spent"]
X = data[used_features].values
scores = data["Score"].values
X_train = X[:11]
X_test = X[11:]
# Logistic Regression - Multiple Classification
level = []
for i in range(len(scores)):
if(scores[i] >= 85):
level.append(2)
elif(scores[i] >= 60):
level.append(1)
else:
level.append(0)
y_train = level[:11]
y_test = level[11:]
classifier = LogisticRegression(C=1e5)
classifier.fit(X_train, y_train)
y_predict = classifier.predict(X_test)
print(y_predict)

