从线性可分 SVM 到线性 SVM
从现实情况引出线性 SVM
线性可分 SVM 学习的训练数据本身就是线性可分的,可以很清晰地在特征向量空间里分成正集和负集。
线性可分 SVM 正负样本之间的间隔叫做“硬间隔”,也就是说在这个“隔离带”里面,肯定不会出现任何训练样本。
我们不难想到,这种情况在现实生活中其实是很少见的。更多的时候,可能是像下面这个样子:
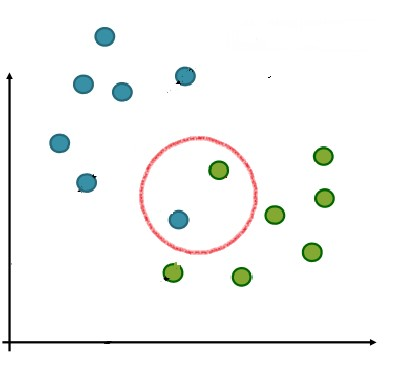
如果没有红圈里那两个点,本来可以很好的分割:
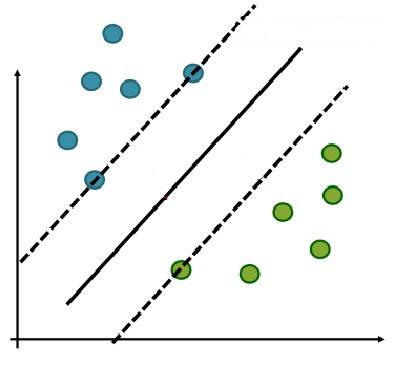
可是偏偏多了那两个点,都找不到分隔超平面了,像下图这样,分来分去,怎么都分不开:
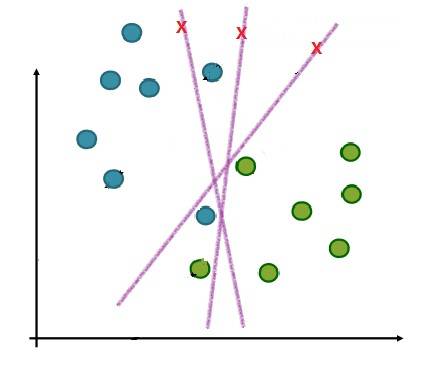
如果不是完全禁止两个辅助超平面之间有任何样本点。而是允许个别样本出现在“隔离带”里面,那样是不是会变得好分得多?比如像下面这样:

这样看起来也很合理。而且,一般情况下,怎么能保证样本就一定能够被分隔得清清楚楚呢?从直觉上我们也觉得,允许一部分样本存在于“隔离带”内更合理。
正是基于这种想法,相对于之前讲的线性可分 SVM 的硬间隔(Hard Margin),人们提出了软间隔(Soft Margin) 的概念。
相应的,对应于软间隔的 SVM,也就叫做线性 SVM。
线性可分 SVM
线性可分 SVM 成立的前提是训练样本在向量空间中线性可分,即存在一个超平面能够将不同类的样本完全彻底,且无一错漏地分开。
用数学式子表达,全部训练样本满足如下约束条件:
$w x_i + b \geqslant 1, \ \ y_i = 1$
$w x_i + b \leqslant 1, \ \ y_i = -1$
这时,$w x_i + b = 1$ 和 $w x_i + b = -1$ 这两个超平面之间的间隔叫做硬间隔。位于它们两个正中的 $w x_i + b = 0$ 是最大分割超平面。
线性 SVM
硬间隔到软间隔
由于样本线性可分的情况在现实当中出现很少,为了更有效地应对实际问题,我们不再要求所有不同类的样本全部线性可分,也就是不再要求硬间隔存在。
取而代之的是将不同类样本之间的硬间隔变成软间隔,即允许部分样本不满足约束条件: $y_i(w x_i + b) \geqslant 1$。
当然,我们还是希望不满足硬间隔条件的样本尽量少,还能够是一个“软”间隔,而非间隔根本不存在。
为了度量这个间隔“软”到何种程度,我们针对每一个样本 $(x_i, y_i)$,引入一个松弛变量 $\xi_i$,令 $\xi_i \geqslant 0$,且 $y_i(wx_i + b) \geqslant 1- \xi_i$。
对应到图形上是这样:
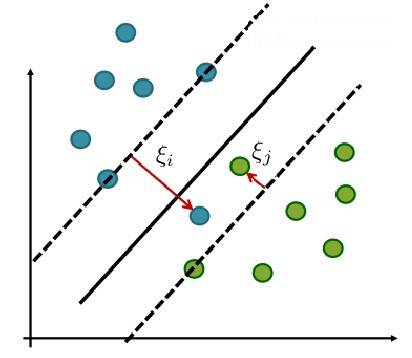
这样看起来,确实比硬间隔合理多了。
优化目标
于是,我们的优化目标就从原来的:
$min_{w,b} \frac{||w||^2}{2} $
$s.t. \ \ \ \ 1 - y_i(w x_i + b) \leqslant 0, \ \ i = 1,2,...,m$
变成了:
$ min_{w,b,\xi} \frac{1}{2}||w||^2 + C\sum_{i=1}^{m}\xi_i $
$ s.t. \ \ \ \ y_i(w x_i + b) \geqslant 1 - \xi_i, \ \ i = 1,2,...,m ; \ \ \xi_i \geqslant 0, \ \ i = 1,2,...,m $
其中 $C$ 是一个大于0的常数,若 $C$ 为无穷大,则 $\xi_i$ 必然为无穷小,否则将无法最小化主问题。如此一来,线性 SVM 就又变成了线性可分 SVM。
当 $C$ 为有限值的时候,才能允许部分样本不遵守约束条件 $1 – y_i(wx_i + b) \leqslant 0$。
这就是线性 SVM 的主问题!
对偶法最优化线性 SVM 主问题
算法思路
上面我们得出了线性 SVM 的主问题。
用对偶法求解线性可分 SVM 的主问题的思路——抽象一下,大致可以分为4个阶段:
Stage-1:根据主问题构建拉格朗日函数,由拉格朗日函数的对偶性,将主问题转化为极大极小化拉格朗日函数的对偶问题。
Stage-2:分步求解极大极小问题。
在每次求解极值的过程中都是先对对应的函数求梯度,再令梯度为0。以此来推导出主问题参数和拉格朗日乘子之间的关系。
再将用拉格朗日乘子表达的主问题参数带回到拉格朗日函数中,最终一步步将整个对偶问题推导为拉格朗日乘子和样本 $(x_i, y_i)$ 之间的关系。
Stage-3:通过最小化拉格朗日乘子与样本量组成的函数(也就是 Stage-2 的结果),求出拉格朗日乘子的值。
这里,可以用 SMO 算法进行求解。
Stage-4:将 Stage-3 求出的拉格朗日乘子的值带回到 Stage-2 中确定的乘子与主问题参数关系的等式中,求解主问题参数。
再根据主问题参数构造最终的分隔超平面和决策函数。
主问题求解
现在我们就按这个思路来对线性 SVM 主问题进行求解。
首先,将主问题写成我们熟悉的约束条件小于等于0的形式,如下:
$ min_{w,b,\xi} \frac{1}{2}||w||^2 + C\sum_{i=1}^{m}\xi_i $
$ s.t. \ \ \ \ 1 - \xi_i - y_i(w x_i + b) \leqslant 0, \ \ i = 1,2,...,m ; \ \ \ \ -\xi_i \leqslant 0, \ \ i = 1,2,...,m $
然后开始逐步求解:
1. 构建拉格朗日函数如下:
$L(w,b,\xi, \alpha, \mu) = \frac{1}{2}||w||^2 + C\sum_{i=1}^{m}\xi_i + \sum_{i=1}^{m}\alpha_i[1-\xi_i - y_i(wx_i +b)] + \sum_{i=1}^{m}(-\mu_i \xi_i)$
$ \alpha_i \geqslant 0,\ \ \mu_i \geqslant 0$
其中 $\alpha_i$ 和 $\mu_i$ 是拉格朗日乘子,而 $w,b$ 和 $\xi_i$ 是主问题参数。
根据主问题的对偶性,主问题的对偶问题是:
$ max_{\alpha,\mu}min_{w,b,\xi}L(w,b,\xi, \alpha, \mu)$
2. 极大极小化拉格朗日函数
(1)极小化
首先 对 $w,b$ 和 $\xi$ 极小化 $L(w,b, \xi, \alpha, \mu)$——分别对 $w,b 和 \xi_i$ 求偏导,然后令导数为0,得出如下关系:
$ w = \sum_{i=1}^{m}\alpha_iy_ix_i $
$ 0 = \sum_{i=1}^{m}\alpha_iy_i $
$ C = \alpha_i + \mu_i $
将这些关系带入线性 SVM 主问题的拉格朗日函数,得到:
$min_{w,b,\xi}L(w,b,\xi, \alpha, \mu) = \sum_{i=1}^{m}\alpha_i - \frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j(x_i \cdot x_j)$
(2)极大化
然后,就要对 $\alpha$ 和 $\mu$ 进行极大化。
因为上面极小化的结果中只有 $\alpha$ 而没有 $\mu$,所以现在只需要极大化 $\alpha$ 就好:
$ max_{\alpha,\mu}min_{w,b,\xi}L(w,b,\xi, \alpha, \mu) = max_\alpha( \sum_{i=1}^{m}\alpha_i - \frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j(x_i \cdot x_j))$
$ s.t. \ \ \ \ \sum_{i=1}^{m}\alpha_iy_i = 0; ;; C - \alpha_i - \mu_i = 0 ;;; \alpha_i \geqslant 0;;; \mu_i \geqslant 0;;; i = 1,2, ..., m$
3. SMO 算法求解对偶问题
我们将上面极大化目标约束条件中的 $\mu$ 用 $\alpha$ 替换掉,并将极大化目标求负转为极小化问题,得到:
$max_\alpha( \sum_{i=1}^{m}\alpha_i - \frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j(x_i \cdot x_j)) = min(\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j(x_i \cdot x_j) - \sum_{i=1}^{m}\alpha_i )$
$ s.t. \ \ \ \ \sum_{i=1}^{m}\alpha_iy_i = 0;;; 0 \leqslant \alpha_i \leqslant C ;;; i = 1,2, ..., m$
我们对照一下上一篇线性可分 SVM 最优化过程中步骤3的结果,不难发现,两者的极小化目标是一样的,所不同的就是约束条件而已。
所以,在上一篇我们用到的 SMO 算法,同样可以用于此处。运用 SMO 求解出拉格朗日乘子 $\alpha_1, \alpha_2, …, \alpha_m$。
4. 根据拉格朗日乘子与主问题参数的关系求解分隔超平面和决策函数
由 $ w = \sum_{i=1}^{m}\alpha_iy_ix_i $ 求出 $w$。
因为最终要求得的超平面满足 $w x + b = 0$,这一点是和线性可分 SVM 的超平面一样的,因此求解 b 的过程也可以照搬:
$ b = \frac{1}{|S|}\sum_{s\in S}(y_s - w x_s)$
其中 $S$ 是支持向量的集合。
线性 SVM 的支持向量
这里有个问题,到底哪些样本算是线性 SVM 的支持向量?
对于线性可分 SVM,支持向量本身是很明确的,就是那些落在最大分隔超平面两侧的两个辅助超平面上的样本。因为样本线性可分,所以这两个辅助超平面中间的硬间隔里,是没有任何样本存在的。
但是,对于线性 SVM,有些不同,这两个辅助超平面中间是软间隔,软间隔的区域内也存在若干样本。这些样本是和辅助超平面上的样本一样算作支持向量呢?还是不算作支持向量?
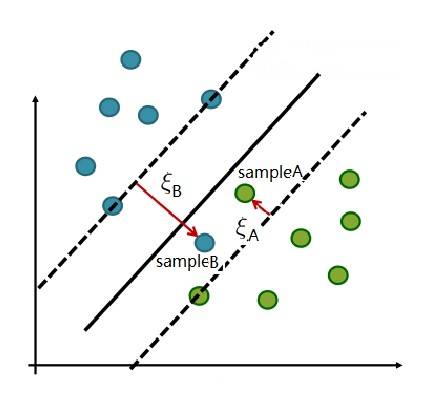
比如下图中的 sampleA 和 sampleB,前者还好,只是“分得不够清楚”, 后者根本就“跨界”到了“对方的地盘”。它们两个到底算不算支持向量呢?
我们先来看看**线性 SVM(又名软间隔 SVM)**主问题拉格朗日函数的 KKT 条件:
$\alpha_i \geqslant 0,;; \mu_i \geqslant 0$
$y_i f(x_i) – 1 + \xi_i \geqslant 0$
$\alpha_i(y_if(x_i) – 1 + \xi_i) = 0$
$\xi_i \geqslant 0$
$\mu_i\xi_i = 0$
其中 $f(x) = wx + b,;; i = 1,2, …, m$
对于任意样本 $(x_i, y_i)$,要么 $\alpha_i = 0$, 要么 $y_i f(x_i) – 1 + \xi_i = 0$。
我们又知道 $w$ 的计算公式为:
$ w = \sum_{i=1}^{m}\alpha_iy_ix_i $
其中拉格朗日乘子为0(即 $\alpha_i = 0$)的项,对于 $w$ 的值是没有影响的,能够影响 $w$ 的,一定是对应拉格朗日乘子大于0的样本。
根据 KKT 条件,这样的样本一定同时满足 $y_if(x_i) – 1 + \xi_i = 0$,也就是 $y_i f(x_i) = 1 – \xi_i$。所有这样的样本,都是线性 SVM 的支持向量。
在满足 $y_i f(x_i) = 1 – \xi_i$ 的前提之下,我们来看 $\xi_i$。
若 $\xi_i = 0$, 则 $y_i f(x_i) = 1$,此时,样本正好落在两个辅助超平面上。所以,两个辅助超平面上的样本,肯定是支持向量。
若 $\xi_i \ne 0$:
当 $\xi_i \leqslant 1$ 时(例如上图中的 $\xi_A$),$1- \xi_i > 0$, $y_i f(x_i) >0$。也就是说 $y_i$ 和 $f(x_i)$ 的结果相乘虽然不为1,但至少这个样本还没有被归错类。
当 $\xi_i > 1$时(例如上图中的 $\xi_B$),$1- \xi_i < 0$,则 $y_i f(x_i) < 0$,这时,样本根本就被归错了类。但是,即使如此,毕竟这样的样本也影响了最终 $w$ 的取值,所以,它也是支持向量。
也就是说,对于线性 SVM 而言,除了落在两个辅助超平面上的样本,落在软间隔之内的样本也是它的支持向量。
非线性分类问题
遇到分类问题的时候,最理想的状态,当然是样本在向量空间中都是线性可分的,我们可以清晰无误地把它们分隔成不同的类别——线性可分 SVM。
如果实在不行,我们可以容忍少数不能被正确划分,只要大多数线性可分就好——线性 SVM。
可是,如果我们面对的分类问题,根本就是非线性的呢?比如像下面这样:

图中红色的点是正类样本,蓝色的点是负类样本。通过我们的观察可知,它们之间的界限是很分明的,用图中绿色的圈本来可以把它们完全分开。
很可惜,“圆圈”在二维空间里无法用线性函数表示,也就是说这些样本在二维空间里根本线性不可分。所以,无论是线性可分 SVM 还是线性 SVM,都无法在这些样本上良好工作。
这可怎么办呢?难道,这种情况我们就处理不了了?
并不是!
我们可以想个办法,让这些在二维空间中线性不可分的样本,在更高维度的空间里线性可分。
比如说,如果我们能把上图中那些正负类的样本映射到三维空间中,并且依据不同的类别给它们赋予不一样的高度值——$z$ 轴取值(就像下图这样),那么不就线性可分了嘛。

如此一来,在二维空间团团转的正负例,在三维空间中分为两层,中间用一个超平面,就可以完美分隔了。
非线性 SVM
非线性 SVM 分隔超平面
对于在有限维度向量空间中线性不可分的样本,我们将其映射到更高维度的向量空间里,再通过间隔最大化的方式,学习得到支持向量机,就是非线性 SVM。
我们将样本映射到的这个更高维度的新空间叫做特征空间。
注意:如果是理想状态,样本从原始空间映射到特征空间后直接就成为线性可分的,那么接下来的学习是可以通过硬间隔最大化的方式来学的。
不过,一般的情况总没有那么理想,因此,通常情况下,我们还是按照软间隔最大化,在特征空间中学习 SVM。
简单理解就是:非线性 SVM = 核技巧 + 线性 SVM。
我们用向量 $x$ 表示位于原始空间中的样本,$\phi(x)$ 表示 $x$ 映射到特征空间之后的新向量。
则非线性 SVM对应的分隔超平面为:$f(x) = w\phi(x) + b$。
非线性 SVM 的对偶问题
套用上一篇线性 SVM 的对偶问题,此处非线性 SVM 的对偶问题就变成了:
$min(\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j\phi(x_i)\cdot \phi(x_j)-\sum_{i=1}^{m}\alpha_i)$
$ s.t. \ \ \ \ \sum_{i=1}^{m}\alpha_iy_i = 0$
$ 0 \leqslant \alpha_i \leqslant C ,\ \ \ \ i = 1,2, ..., m$
大家可以看到,和线性 SVM 唯一的不同就是:之前的 $x_i$ 与 $x_j$ 的内积(点乘) 变成了 $\phi(x_i)$ 与 $\phi(x_j)$ 的内积。
核函数
对于有限维的原始空间,一定存在更高维度的空间,使得前者中的样本映射到新空间后可分。但是新空间(特征空间)的维度也许很大,甚至可能是无限维的。这样的话,直接计算 $\phi(x_i)·\phi(x_j)$ 就会很困难。
为了避免计算 $\phi(x_i)$ 和 $\phi(x_j)$ 的内积,我们需要设置一个新的函数——$ k(x_i, x_j)$:
$ k(x_i, x_j) =\phi(x_i) \cdot \phi(x_j) $
原始空间中的两个样本 $x_i$ 和 $x_j$ 经过 $k(·,·)$ 函数计算所得出的结果,是它们在特征空间中映射成的新向量的内积。
如此一来,我们就不必真的计算出 $\phi(x_i)$ 点乘 $\phi(x_j)$ 的结果,而可以直接用 $k(·,·)$ 函数代替它们。
我们把这个 $k(·,·)$ 函数叫做核函数。现在我们给出它的正式定义:
设 $ \mathcal{X}$ 为原始空间(又称输入空间),$\mathcal{H}$ 为特征空间(特征空间是一个带有内积的完备向量空间,又称完备内积空间或希尔伯特空间)。
如果存在一个映射: $ \mathcal{X} \times \mathcal{X}$ ,使得对所有 $ x_i, x_j \in \mathcal{X} $,函数 $ k(x_i, x_j)$ 满足条件:$ k(x_i, x_j) =\phi(x_i) \cdot \phi(x_j) $,即 $k(·,·)$ 函数为输入空间中任意两个向量映射到特征空间后的内积。
则称 $k(·,·)$ 为核函数,$\phi(·)$ 为映射函数。
运用核技巧求解非线性 SVM 的对偶问题
有了核函数,我们就可以将非线性 SVM 的对偶问题写成:
$min(\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j k(x_i, x_j) - \sum_{i=1}^{m}\alpha_i )$
$ s.t. \ \ \ \ \sum_{i=1}^{m}\alpha_iy_i = 0$
$ 0 \leqslant \alpha_i \leqslant C ,\ \ \ \ i = 1,2, ..., m$
之后的求解过程与线性 SVM 一致:先根据对偶问题求解 $\alpha$,再根据 $\alpha$ 的结果计算 $w$,然后根据支持向量求解 $b$,在此就不赘述了。
相应的,最终求出的非线性 SVM 在特征空间的最大分隔超平面也就成了:
$ f(x) = w \phi(x) + b = \sum_{i=1}^{m}\alpha_i y_i \phi(x_i)\cdot \phi(x) + b = \sum_{i=1}^{m}\alpha_i y_i k(x, x_i) + b$
上述运用核函数求解的过程,称为核技巧。
核函数的性质
如果我们已经知道了映射函数是什么,当然可以通过两个向量映射后的内积直接求得核函数。
但是,在我们还不知道映射函数本身是什么的时候,有没有可能直接判断一个函数是不是核函数呢?
换句话说,一个函数需要具备怎样的性质,才是一个核函数?
以下是函数 $k(·,·)$ 可以作为核函数的充分必要条件:
设 $ \mathcal{X}$ 是输入空间,$k(·,·)$ 是定义在 $ \mathcal{X} \times \mathcal{X}$ 上的对称函数,当且仅当任意 $ x_1, x_2, ..., x_m \in \mathcal{X} $, 核矩阵 $K$(如下所示)总是半正定时,$k(·,·)$ 就可以作为核函数使用。
核矩阵:
$K=\left[ \begin{matrix} k(x_1,x,1) & ... & k(x_1,x,j) & ... & k(x_1,x,m) \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ k(x_i,x,1)& ... & k(x_i,x,j) & ... & k(x_i,x,m) \\ \vdots & \ddots & \vdots & \ddots &\vdots \\ k(x_m,x_1)& ... & k(x_m,x_j) & ... & k(x_m,x_m) \end{matrix} \right]$
注意:这里有几个线性代数的基础概念,请见下。
对称函数:函数的输出值不随输入变量的顺序改变而改变的函数叫做对称函数。
因为输入空间中的 $x_i 和 x_j$ 是向量,特征空间中的 $\phi(x_i) 和 \phi(x_j)$ 也是向量,$k(x_i,x_j)$ 表示特征空间向量的内积,而两个向量的内积并不因为其顺序变化而变化。因此,$ k(x_i,x_j) = k(x_j,x_i)$,即 k$(·,·)$ 为对称函数。
相应的,核矩阵 K 为对称矩阵。
半正定矩阵:一个 $n \times n$ 的实对称矩阵 $M$ 为半正定,当且仅当对于所有非零实系数向量 $z$,均有: $ z^TMz \geqslant 0$。
其中“非零实系数向量”的含义是:一个向量中所有元素均为实数,且其中至少有一个元素值非零。
核函数的种类
要知道,非线性 SVM 的关键在于将输入空间中线性不可分的样本映射到线性可分的特征空间中去。特征空间的好坏直接影响到了 SVM 的效果。
如何选择核函数也就成了一个关键性的问题。
虽然我们已经学习了核函数的定义和性质,但让我们凭空去自己构建一个核函数出来,还是一个非常困难的任务。
即使真得构造出来了,这个核函数在具体问题上的效果如何,还需要通过大量测试来证明,很可能费了好大劲,最后效果还不理想。
好在前人已经给我们留下来一些经历了长久磨练的常用核函数,让我们可以直接拿来用。接下来,我们分别看下这些核函数。
线性核(Linear Kernel)
$k(x_i, x_j) = x_i^Tx_j$
使用时无须指定参数(Parameter),它直接计算两个输入向量的内积。经过线性核函数转换的样本,特征空间与输入空间重合,相当于并没有将样本映射到更高维度的空间里去。
很显然这是最简单的核函数,实际训练、使用 SVM 的时候,在不知道用什么核的情况下,可以先试试线性核的效果。
多项式核(Polynomial Kernel)
$k(x_i, x_j) = (\gamma x_i^Tx_j + r)^d, \ \ \ \ \gamma > 0,\ \ d \geqslant 1$
需要指定三个参数:$\gamma$,$r$ 和 $d$。
这是一个不平稳的核,适用于数据做了归一化(Normalization,参见本文最后一节)的情况。
RBF 核(Radial Basis Function Kernel)
$k(x_i, x_j) = \exp(-\gamma||x_i - x_j||^2) , \ \ \ \ \gamma > 0$
RBF 核又名高斯核 (Gaussian Kernel),是一个核函数家族。它会将输入空间的样本以非线性的方式映射到更高维度的空间(特征空间)里去,因此它可以处理类标签和样本属性之间是非线性关系的状况。
它有一个参数:$\gamma$,这个参数的设置非常关键!
如果设置过大,则整个 RBF 核会向线性核方向退化,向更高维度非线性投影的能力就会减弱;但如果设置过小,则会使得样本中噪音的影响加大,从而干扰最终 SVM 的有效性。
不过相对于多项式核的3个参数,RBF 核只有一个参数需要调,还是相对简单的。
当线性核效果不是很好时,可以用 RBF 试试。或者,很多情况下可以直接使用 RBF。
著名的 LIBSVM(台湾大学林智仁/Lin Chih-Jen 教授等设计开发的一款简单、易用、快速有效的 SVM/SVR 支持包)的默认核函数,就是 RBF 核。
Sigmoid 核(Sigmoid Kernel)
$k(x_i, x_j) = tanh(\gamma x_i^Tx_j + r)$
有两个参数,$\gamma$ 和 $r$,在某些参数设置之下,Sigmoid 核矩阵可能不是半正定的,此时 Sigmoid 核也就不是有效的核函数了。因此参数设置要非常小心。
整体而言,Sigmoid 核并不比线性核或者 RBF 核更好。但是,当参数设置适宜时,它会有不俗的表现。
在具体应用核函数时,最好针对具体问题参照前人的经验。
构建自己的核函数
除了常见的核函数,我们还可以根据以下规律进行核函数的组合。
-
与正数相乘:
$k(·,·)$ 是核函数,对于任意正数(标量)$\alpha \geqslant 0, ;; \alpha k(·,·)$ 也是核函数。 -
与正数相加:
$k(·,·)$ 是核函数,对于任意正数(标量)$\alpha \geqslant 0, ;; \alpha + k(·,·)$ 也是核函数。 -
线性组合:
$k(·,·)$ 是核函数,则如下线性组合也是核函数:$ \sum_{i=1}^{n}\alpha_i k_i(\cdot ,\cdot), \ \ \ \ \alpha_i \geqslant 0$。 -
乘积:
$k_1(·,·)$ 和 $k_2(·,·)$ 都是核函数,则它们的乘积——$k_1(·,·) k_2(·,·)$——也是核函数。 -
正系数多项式函数:
设 $P$ 为实数域内的正系数多项式函数,$k(·,·)$ 是核函数,则 $P(k(·,·))$ 也是核函数。 -
指数函数:
$k(·,·)$ 是核函数,则 $\exp{(k(·,·))}$ 也是核函数。
掌握了这些规律,我们也可以尝试根据需要构建自己的核函数。
数据归一化(Data Normalization)
数据归一化是一种数据处理方法,具体所做的就是对取值范畴不同的数据进行归一化处理,使它们处在同一数量级上。
最常见的,就是把各种数据都变成 $(0,1)$ 之间的小数。
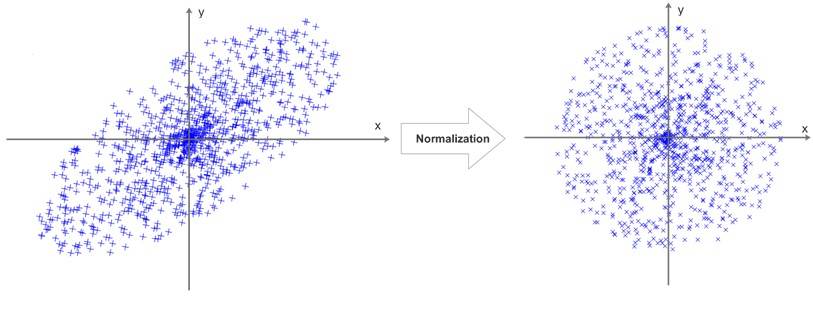
上图是一个归一化过程在二维中的直观显示。
大家可以看到, “扁长”的数据分布,经过归一化处理之后,变成了一个“正圆”。
常用的归一化算法有:
(1)线性转换
$x' = \frac{(x - min)}{(max - min)}$
(2)标准分
$x'= \frac{(x – \mu)}{\gamma}$
原本的 $x$ 符合正态分布,$\mu$ 为其分布的均值,而 $\gamma$ 为分布的方差。

