一般情况下,我们就用 $x$ 代表一个函数的自变量。这个 $x$ 本身可以是多维的。
而且,同一个函数可能同时既有等式约束条件,又有不等式约束条件。
主问题
现在我们考虑在 $d$ 维空间上有 $m$ 个等式约束条件和 $n$ 个不等式约束条件的极小化问题。这样的问题可以写作:
$min f(x),\ 其中\ x\ 为\ d\ 维$。
$s.t. \ \ h_i(x) = 0 , \ \ i = 1,2,…, m; \ \ g_j(x) \leqslant 0, \ \ j = 1,2, …, n$
我们把上述问题称为“原始最优化问题”,也可以叫做“原始问题”或“主问题”。
为了解决原始问题,我们引入拉格朗日乘子 $\lambda = (\lambda_1, \lambda_2, …, \lambda_m)^T $ 和 $\mu = (\mu_1, \mu_2, …, \mu_n)^T $,构造拉格朗日函数为:
$L(x,\lambda,\mu) = f(x) + \sum_{i=1}^{m}\lambda_ih_i(x) + \sum_{j=1}^{n}\mu_jg_j(x) $
然后,再设:
$\Gamma(\lambda,\mu) = inf_{x\in D}( f(x) + \sum_{i=1}^{m}\lambda_ih_i(x) + \sum_{j=1}^{n}\mu_jg_j(x)) $
其中,$x \in D$,$D$ 为主问题可行域;$inf(L)$ 表示 $L$ 函数的下确界,$inf(L(x, \lambda, \mu))$ 表示小于或者等于 $L(x, \lambda, \mu)$ 的极大值。
$h_i(x) = 0$,因此对于任意 $\lambda_i$,必然有:
$\sum_{i=1}^{m}\lambda_ih_i(x) = 0$, 其中 $i=1,2,…, m$。
又因为 $g_j(x) \leqslant 0$,因此对于 $\mu_j$ 均为非负的情况:$\mu_j \geqslant 0$,必然有:
$\sum_{j=1}^{n}\mu_jg_j(x) \leqslant 0$, 其中 $j=1,2,…, n$。
假设 $\hat x$ 是主问题可行域中的一个点,则对于任意 $\mu_j \geqslant 0 , \ \ j=1,2,…, n$ 和任意 $\lambda_i , \ \ i=1,2,…, m$,有:
$\Gamma(\lambda,\mu) \leqslant L(\hat x, \lambda, \mu) \leqslant f(\hat x)$
我们假设主问题的最优解是 $p^* $,也就是说 $p^* $ 是 $f(\hat x)$ 所有取值中极小的那个。
又因为所有 $\hat x$ 对于任意 $\mu_j \geqslant 0 , \ \ j=1,2, …, n$ 和任意 $\lambda_i, \ \ i=1,2,…, m$,有:
$\Gamma(\lambda,\mu) \leqslant f(\hat x)$
因此,对于任意 $\mu_j \geqslant 0 , \ \ j=1,2,…, n$ 和任意 $\lambda_i, \ \ i=1,2,…, m$ 有 $\Gamma(\lambda,\mu) \leqslant p^* $,也就是说,$\Gamma(\lambda, \mu)$ 是主问题最优解的下确界。
对偶函数和对偶问题
在此,我们把 $\Gamma(\lambda,\mu)$ 称为对偶函数。
对偶函数和目标函数最优解(极小值)的关系如下:
$\Gamma_{\lambda,\mu;\mu_j\geqslant0}(\lambda,\mu) \leqslant p^* $
由上式子得出:
$max(\Gamma_{\lambda,\mu;\mu_j\geqslant0}(\lambda,\mu)) \leqslant p^* $
这里的:
$max(\Gamma_{\lambda,\mu;\mu_j\geqslant0}(\lambda,\mu)) $
我们称为主问题的对偶问题,$\lambda$ 和 $\mu$ 称为对偶变量。
强对偶性及求解对偶问题
设对偶问题的最优解为 $d^* $,显然有 $d^* \leqslant p^* $。
若 $d^* ==p^* $,则我们将主问题和对偶问题的关系称为强对偶性,否则称为弱对偶性。
显然,强对偶性如果成立,我们就可以通过最优化对偶问题来达到最优化主问题的目的了。
那么什么时候强对偶性成立呢?
如果主问题是凸优化问题,也就是说当:
- 拉格朗日函数中的 $f(x) 和 g_j(x)$ 都是凸函数;
- $h_i(x)$ 是仿射函数;
- 主问题可行域中至少有一点使得不等式约束严格成立。即存在 $x$,对所有 $j$,均有 $g_j(x)<0$。
1、2、3 同时成立时,强对偶性成立。
注意:当主问题和对偶问题存在强对偶性时,存在 $x^* $,$\lambda^* $ 和 $\mu^* $ 分别为主问题的解和对偶问题的解的充分必要条件是:它们满足 KKT 条件!
通过对偶问题求解主问题
当强对偶性成立时,为了解决主问题,我们可以这样做:
- 构造拉格朗日函数,引入非负参数的拉格朗日算子去给目标函数加上限制;
- 求拉格朗日函数对主变量的极小——将拉格朗日函数对主变量求偏导,令其为零后得出主变量与对偶变量的数值关系,由此把对主变量进行极小化的拉格朗日函数转化为一个对偶变量的函数;
- 求上面第2步得出的函数对对偶变量的极大
由此一来,就将求解主问题转化成了极大极小问题。
下面,我们就用这个方法来求解线性可分 SVM 的目标函数。
线性可分 SVM 的对偶问题
主问题
线性可分 SVM 的主问题为:
$\ min_{w,b} \frac{||w||^2}{2} $
$\ s.t. \ \ \ \ g_i(w,b) = 1 - y_i(w x_i + b) \leqslant 0, \ \ i = 1,2,...,m$
主问题的强对偶性
我们需要判断一下线性可分 SVM 主问题是否是强对偶的。
因为:
- $f(w,b) = \frac{||w||^2}{2}$ 是凸函数;
- $g_i(w,b) = 1 – y_i(w x_i + b)$ 也是凸函数(没错,线性函数是凸函数!);
- 想想我们是如何构造不等式约束条件的——对于所有位于最大分割超平面两侧,距离最大分割超平面距离为 $||w||$ 的辅助超平面上的点 $x^* $,有 $1- y^* (w x^* + b) = 0$, 而对这两个辅助平面之外的点 $x^{}$,则有 $1 – y^{} (w x^{**} + b) < 0$。因此,主问题可行域中,至少有一点使得不等式条件严格成立。
所以,线性可分 SVM 的目标函数可以通过求解其对偶问题来求解。
使用对偶算法求解线性可分 SVM 的步骤
步骤1:对主问题构造拉格朗日函数。
引入拉格朗日乘子 $\alpha_i \geqslant 0,其中 i=1,2,…, m$,得到拉格朗日函数:
$L(w,b,\alpha) = \frac{1}{2}||w||^2 + \sum_{i=1}^{m}\alpha_i[1- y_i(wx_i +b)] $
步骤2:求拉格朗日函数对于 $w$,$b$ 的极小。
注意:这里要用到一个向量求导的小知识—— 有向量 $X=(x_1,x_2,...,x_n)$,则 $X$ 的函数 $f(X)$ 对 $X$ 的导数为:
$\frac{df(X)}{dX} = (\frac{df}{dx_1}, \frac{df}{dx_2}, ..., \frac{df}{dx_n})$
因为 $w$ 为向量,假设 $w=(w_1,w_2,…,w_n)$,有:
$||w|| = \sqrt{(w_1^2 + w_2^2 + … + w_n^2)}$
则:
$||w||^2 = w_1^2 + w_2^2 + … + w_n^2$
因此,$f(w) = \frac{||w||^2}{2}$ 对 $w$ 求导结果为:$\frac{df(w)}{dw} = (w_1,w_2, …, w_n) = w$
我们先将拉格朗日函数对 $w$ 和 $b$ 求偏导,然后分别令两个偏导结果为0,之后得出了下列数值关系:
$ w = \sum_{i=1}^{m}\alpha_iy_ix_i $
$ 0 = \sum_{i=1}^{m}\alpha_iy_i $
将这两个等式带入拉格朗日函数,得:
$L(w,b,\alpha) = \frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j(x_i \cdot x_j) + \sum_{i=1}^{m}\alpha_i - \sum_{i=1}^{m}\alpha_iy_i((\sum_{j=1}^{m}\alpha_jy_jx_j)\cdot x_i + b) = \sum_{i=1}^{m}\alpha_i - \frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j(x_i \cdot x_j) $
也就是:
$ min_{w,b}L(w,b,\alpha)= \sum_{i=1}^{m}\alpha_i - \frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j(x_i \cdot x_j) $
步骤3:求 $min_{w,b}L(w,b,\alpha)$ 对 $\alpha$ 的极大。
也就是对偶问题:
$ max_\alpha min_{w,b}L(w,b,\alpha) $
$s.t. \sum_{i=1}^{m}\alpha_i y_i = 0 $
$\alpha_i \geqslant 0, \ \ i =1,2,...,m $
又因为:
$ max_\alpha min_{w,b}L(w,b,\alpha) = max_\alpha [\sum_{i=1}^{m}\alpha_i - \frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j(x_i \cdot x_j)] = min_\alpha [\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j(x_i \cdot x_j) - \sum_{i=1}^{m}\alpha_i] $
因此对偶最优化问题变成了:
$min_\alpha [\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j(x_i \cdot x_j) - \sum_{i=1}^{m}\alpha_i] $
$s.t. \sum_{i=1}^{m}\alpha_i y_i = 0 $
$\alpha_i \geqslant 0,\ \ i =1,2,...,m $
步骤4:由对偶问题求 $\alpha_1, \alpha_2,…, \alpha_m$。
设:$T(\alpha_1, \alpha_2,...,\alpha_m) = \frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j(x_i \cdot x_j) - \sum_{i=1}^{m}\alpha_i$
注意:上面这个函数中,$x_i, x_j, y_i, y_j$ 都是训练样本的 $x$ 和 $y$ 值,都是定值我们只需带入即可,因此这是一个关于 $\alpha_1, …, \alpha_m$ 的函数。
要最小化 $T(\alpha_1, \alpha_2, …, \alpha_m)$,我们可以把 $\alpha$ 看作一个向量:$\alpha = (\alpha_1, \alpha_2, …, \alpha_m)$,我们要通过基于约束条件 $\sum(a_iy_i)=0$ 最小化 $f(\alpha)$,来求 $\alpha$ 的最优解 $\alpha^* $。
我们可以对 $\alpha_1, \alpha_2,…, \alpha_m$ 分别求偏导,然后令偏导为0 ,再结合约束条件来求 $\alpha$ 的最优解:$\alpha^* = (\alpha_1^* , \alpha_2^* , …, \alpha_m^* )$。
此处可以采取 SMO 算法,SMO 的具体内容我们在本文最后进行讲解,此处跳过,总之到这一步,我们已经求出了$ \alpha^* $ 。
步骤5:由 $ \alpha ^* $ 求 $w$。
由步骤1已知:
$ w = \sum_{i=1}^{m}\alpha_iy_ix_i $
$x_i,y_i$ 已知, $\alpha_i^* $ 已由上一步求出,将它们带入上式,求 $w$。
步骤6:由 $w$ 求 $b$。
$\alpha_1*, \alpha_2*, …, \alpha_m*$ 都已经求出来了。
因为 $\alpha_i(1- y_i(wx_i + b))= 0; \ \ i = 1,2, …, m$ 是整体约束条件;又因为对于所有支持向量 $(x_s,y_s)$,都有 $1 - y_s(w x_s + b) = 0$,因此,所有大于0的 $\alpha_k^* $ 所对应的 $ (x_k, y_k)$ 必然是支持向量。
否则,如果 $\alpha_k^* > 0, 1- y_k(wx_k + b) < 0$,则 $\alpha_k^* (1- y_k(wx_k + b)) <0$,不符合约束条件。
注意:我们再推想一下,会不会所有的 $\alpha_i^* $ 都等于0呢?
如果那样的话,根据步骤5中的 $w$ 计算公式,得 $w = 0,||w|| = 0$,则 $\frac{2}{||w||}$ 趋近正无穷,而 $\frac{2}{||w||}$ 的物理意义是两个线性可分数据集之间的最大距离。
我们希望这个距离尽量大是希望两个集合被分得尽量清楚,而如果两个集合之间的距离都是无穷了,又怎么能说它们处在相同的特征空间里呢?
还有,我们原本定义的两个辅助超平面是 $wx + b = 1$ 和 $wx + b = -1$,如果 $w=0$,则 $b=1$ 和 $b=-1$同时成立,这显然矛盾了。所以 $w$ 肯定不为0,因此必然存在 $\alpha_k^* > 0$。
那么既然哪些 $(x, y)$ 对是支持向量都已经清楚了,理论上讲,我们随便找一个支持向量 $(x_s,y_s)$,把它和 $w$ 带入:$y_s(wx_s + b) = 1$,求出 $b$ 即可。
$y_s(wx_s) + y_sb = 1$,两边乘以 $y_s$。
$y_s^2(wx_s) + y_s^2b = y_s$,因为 $y_s^2 = 1$,所以:$b = y_s – w x_s$。
为了更加鲁棒,我们可以求所有支持向量的均值:
$ b = \frac{1}{|S|}\sum_{s\in S}(y_s - w x_s)$
步骤7: 求最终结果。
构造最大分割超平面:$wx + b = 0$。
构造分类决策函数:$f(x) = sign(wx + b)$。
其中,$sign(\cdot)$ 全称为 Signum Function。其定义为:
$\displaystyle \operatorname {sign} (x)=\left\{\begin{matrix}-1&:&x<0 \\ 0&:&x=0 \\ 1&:&x>0\end{matrix}\right.$
SMO(Sequential Minimal Optimization)算法
先来看一下我们的优化目标:
$T(\alpha_1, \alpha_2,...,\alpha_m) = \frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j(x_i \cdot x_j) - \sum_{i=1}^{m}\alpha_i$
$min_\alpha T(\alpha_1, \alpha_2, ..., \alpha_m) $
$s.t. \sum_{i=1}^{m}\alpha_i y_i = 0 $
$\alpha_i \geqslant 0, i =1,2,...,m $
一共有 $m$ 个参数需优化。
这是一个典型的二次规划问题,我们可以直接用二次规划方法求解。或者,为了节约开销我们也可以用 SMO 算法。
SMO 是一种动态规划算法,它的基本思想非常简单:每次只优化一个参数,其他参数先固定住,仅求当前这一个优化参数的极值。
可惜,我们的优化目标有约束条件:$\sum(\alpha_iy_i) = 0,其中 i = 1,2,…,m$。如果我们一次只优化一个参数,就没法体现约束条件了。
于是,我们这样做:
1. 选择两个需要更新的变量 $\alpha_i$ 和 $\alpha_j$,固定他们以外的其他变量。
这样,约束条件就变成了:
$\alpha_i y_i + \alpha_j y_j = c, \alpha_i \geqslant 0, \alpha_j \geqslant 0 $
其中:
$ c = - \sum_{k\ne i,j} \alpha_k y_k$
这样由此,可得出 $\alpha_j = \frac{(c – \alpha_i y_i)}{y_j}$,也就是我们可以用 $\alpha_i$ 的表达式代替 $\alpha_j$。
将这个替代式带入优化目标函数。就相当于把目标问题转化成了一个单变量的二次规划问题,仅有的约束是 $c \geqslant \alpha_i \geqslant 0$。
2. 对于仅有一个约束条件的最优化问题,我们完全可以在 $\alpha_i$ 上,对问题函数 $T(\alpha_i)$ 求(偏)导,令导数为零,从而求出变量值 $\alpha_{i_{new}}$。
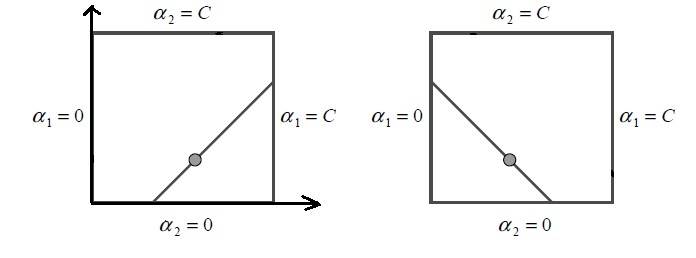
注意:需要注意的是求出的变量值 $\alpha_{i_{new}}$ 还要考虑限制条件 $0 \leqslant \alpha_i \leqslant c$,$\alpha_i$ 的取值要满足直线 $\alpha_i y_i + \alpha_j y_i = y_i c$ 落在 $[0,c] \times [0, c]$ 的矩形中的部分(参照下图):
检查 $\alpha_{i_{new}}$ 是否在这个区域内,如果不在,只能取这个区域边界上让问题函数达到相对最小的点作为新值。
确定新值后,更新 $\alpha_i$ 和 $\alpha_j$。
3. 多次迭代上面1-2步, 直至收敛。